Question

Find the angle between minute and hour hand at 9’o clock.

Answer 1

Hint: Put the hour hand at number ‘9’ in the clock and minutes hand at 12. Now, draw a diagram with the help of it and try to relate the angle between them. Angle between two consecutive numbers in a clock is ${{30}^{\circ }}$ .Use this information to solve the problem.

Complete step-by-step answer:
As we know the positions of hour hand and minutes hands, so by representing it in a diagram of a clock showing 9 o'clock, we can get angles between hour and minute hand.
As we know, an hour hand at any perfect time (2’o clock, 3 o'clock, 9 o'clock etc.) will lie on that particular number or position in the clock.
And minutes at any perfect time will always lie on number 12.
So, we get that hour hand will lie at ‘9’ in the clock and minutes hand will lie at number 12.
So, we can draw a diagram as

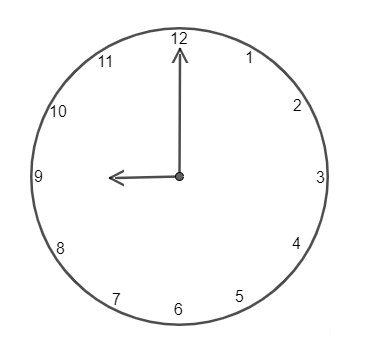
Now, as we know the total angle at the centre of the circle is ${{360}^{\circ }}$ i.e. a complete rotated angle. As, we can observe that there are 12 equal gaps between the numbers. Hence, angle between any two successive number will be $\dfrac{{{360}^{\circ }}}{12}={{30}^{\circ }}$ .Hence, the angle with three gaps (9 to 10, 10 to 11, 11 to 12) will be given as 30 x 3 = ${{90}^{\circ }}$. And another angle at 9 o'clock can be given with the help of reflex angle concept.
Hence, reflex angle formed at centre would be $360-90={{270}^{\circ }}$
Hence, ${{90}^{\circ }}$ and ${{270}^{\circ }}$ are two angles between minutes and hour hand at 9 o'clock.

Note: Using the concept that the angle between two numbers in the clock will be ${{30}^{\circ }}$ always. So, be clear with it and use It for next upcoming questions of this type.Go with the fundamental concepts of hours hand and minutes hand. Don’t try to guess the angle between them.