
Find the angle between the curves
Answer
525.9k+ views
Hint:Calculate the point of intersection of two curves. Calculate the slope of the tangent of both the curves at their point of intersection by finding the value of the first derivative of the curve at the point of intersection. Use the formula
Complete step-by-step answer:
We have to calculate the angles between the curves
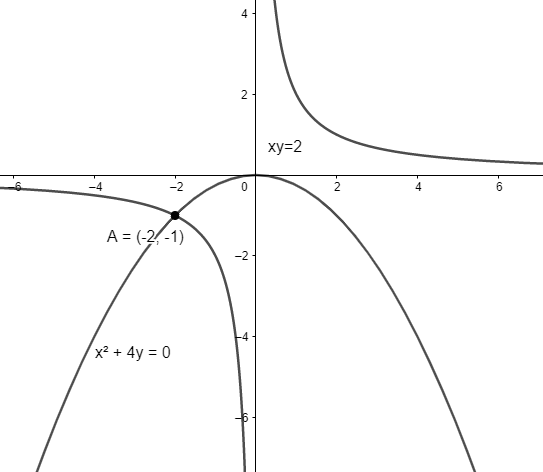
We will first find the point of intersection of the two curves.
We know that
Thus, we have
So, we have
Substituting equation (1) in the equation
Thus, the point of intersection of two curves is
We know that the angle between the two curves is the angle between the tangents of both the curves at their point of intersection.
We will now calculate the slope of tangents of both the curves at their point of intersection. To do so, we will calculate the value of the first derivative of both the curves at the point of intersection.
We will first consider the curve
We know that differentiation of any function of the form
Thus, for
We will now calculate the slope of the tangent of the curve
Thus, we have
Thus, the slope of tangents of the curves
We will now calculate the angle between the tangents at the point of intersection of the two curves.
We know that angle between two tangents with slopes
Substituting
Simplifying the above expression, we have
Taking inverse on both sides, we have
Hence, the angle between the curves
Note: We can’t solve this question without using the fact that the angle between the two curves is the angle between the tangents of both the curves at their point of intersection. We can also solve this question by writing the exact equation of tangents at the point of intersection of two curves and then calculating the angles between them.
Complete step-by-step answer:
We have to calculate the angles between the curves

We will first find the point of intersection of the two curves.
We know that
Thus, we have
So, we have
Substituting equation (1) in the equation
Thus, the point of intersection of two curves is
We know that the angle between the two curves is the angle between the tangents of both the curves at their point of intersection.
We will now calculate the slope of tangents of both the curves at their point of intersection. To do so, we will calculate the value of the first derivative of both the curves at the point of intersection.
We will first consider the curve
We know that differentiation of any function of the form
Thus, for
We will now calculate the slope of the tangent of the curve
Thus, we have
Thus, the slope of tangents of the curves
We will now calculate the angle between the tangents at the point of intersection of the two curves.
We know that angle between two tangents with slopes
Substituting
Simplifying the above expression, we have
Taking inverse on both sides, we have
Hence, the angle between the curves
Note: We can’t solve this question without using the fact that the angle between the two curves is the angle between the tangents of both the curves at their point of intersection. We can also solve this question by writing the exact equation of tangents at the point of intersection of two curves and then calculating the angles between them.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Which one of the following is a true fish A Jellyfish class 12 biology CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Write the difference between solid liquid and gas class 12 chemistry CBSE




