
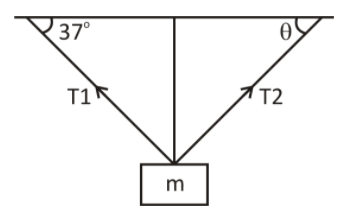
Find the angle $\theta $ if ${T_2} = 2{T_1}$
A.${\cos ^{ - 1}}\left( {\dfrac{2}{5}} \right)$
B.${\cos ^{ - 1}}\left( {\dfrac{1}{5}} \right)$
C.${\sin ^{ - 1}}\left( {\dfrac{1}{3}} \right)$
D.None of these

Answer
476.1k+ views
Hint: As the body is in equilibrium, horizontal components of ${T_1}$ and ${T_2}$balance. Hence we can equate –
${T_1}\sin {\theta _1} = {T_2}\sin {\theta _2}$
In such questions the balancing of the horizontal and vertical components are to be done and the value of the unknown term is found out.
Complete Step by step answer: Given: The angle made by first rope with horizontal base ceiling= ${\theta _1} = 37^\circ $
Mass of the object suspended by ropes is: $m$
${T_1}$= tension in the first rope due to mass of the body
${T_2}$= tension in the second rope to the mass of the body
${T_2} = 2{T_1}$
From the given question, an object is hanged by a ceiling with two ropes. Due to weight of object strain and stress is created in the rope. The ${\theta _1}$is the angle made by the first rope with horizontal base ceiling and ${\theta _2}$is the angle made by the second rope with horizontal base ceiling.
As the body is in equilibrium, horizontal components of ${T_1}$ and ${T_2}$balance. Hence we can equate –
${T_1}\sin {\theta _1} = {T_2}\sin {\theta _2}$…………………………………………………………………………. (I)
Whereas ${\theta _1}$is the angle made by first rope with horizontal base ceiling
And ${\theta _2}$is the angle made by second rope with horizontal base ceiling
${T_1}\sin 37^\circ = {T_2}\sin {\theta _2}$
$\Rightarrow {T_1}\sin 37^\circ = 2{T_1}\sin {\theta _2}$
$\Rightarrow \sin 37^\circ = 2\sin {\theta _2}$
$\Rightarrow \sin {\theta _2} = \dfrac{{\sin 37^\circ }}{2}$
$\Rightarrow \sin {\theta _2} = \dfrac{{0.6018}}{2}$
$\Rightarrow \sin {\theta _2} = 0.3009$
$\Rightarrow {\theta _2} = {\sin ^{ - 1}}(0.3009)$
Hence, none of the answers (A), (B) and (C) is correct.
Hence option (D) is the correct answer.
Note: In such questions the most important things to take care is that the components of forces taken must be equated with the correct component of the other forces. We should also have the idea that Stress and strain are two different terms. Stress is the force acting on the unit area of the surface or material whereas the strain is the effect of stress. Stress can deform the body.
${T_1}\sin {\theta _1} = {T_2}\sin {\theta _2}$
In such questions the balancing of the horizontal and vertical components are to be done and the value of the unknown term is found out.
Complete Step by step answer: Given: The angle made by first rope with horizontal base ceiling= ${\theta _1} = 37^\circ $
Mass of the object suspended by ropes is: $m$
${T_1}$= tension in the first rope due to mass of the body
${T_2}$= tension in the second rope to the mass of the body
${T_2} = 2{T_1}$
From the given question, an object is hanged by a ceiling with two ropes. Due to weight of object strain and stress is created in the rope. The ${\theta _1}$is the angle made by the first rope with horizontal base ceiling and ${\theta _2}$is the angle made by the second rope with horizontal base ceiling.
As the body is in equilibrium, horizontal components of ${T_1}$ and ${T_2}$balance. Hence we can equate –
${T_1}\sin {\theta _1} = {T_2}\sin {\theta _2}$…………………………………………………………………………. (I)
Whereas ${\theta _1}$is the angle made by first rope with horizontal base ceiling
And ${\theta _2}$is the angle made by second rope with horizontal base ceiling
${T_1}\sin 37^\circ = {T_2}\sin {\theta _2}$
$\Rightarrow {T_1}\sin 37^\circ = 2{T_1}\sin {\theta _2}$
$\Rightarrow \sin 37^\circ = 2\sin {\theta _2}$
$\Rightarrow \sin {\theta _2} = \dfrac{{\sin 37^\circ }}{2}$
$\Rightarrow \sin {\theta _2} = \dfrac{{0.6018}}{2}$
$\Rightarrow \sin {\theta _2} = 0.3009$
$\Rightarrow {\theta _2} = {\sin ^{ - 1}}(0.3009)$
Hence, none of the answers (A), (B) and (C) is correct.
Hence option (D) is the correct answer.
Note: In such questions the most important things to take care is that the components of forces taken must be equated with the correct component of the other forces. We should also have the idea that Stress and strain are two different terms. Stress is the force acting on the unit area of the surface or material whereas the strain is the effect of stress. Stress can deform the body.
Recently Updated Pages
The correct geometry and hybridization for XeF4 are class 11 chemistry CBSE

Water softening by Clarks process uses ACalcium bicarbonate class 11 chemistry CBSE

With reference to graphite and diamond which of the class 11 chemistry CBSE

A certain household has consumed 250 units of energy class 11 physics CBSE

The lightest metal known is A beryllium B lithium C class 11 chemistry CBSE

What is the formula mass of the iodine molecule class 11 chemistry CBSE

Trending doubts
State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

How do I convert ms to kmh Give an example class 11 physics CBSE

Give an example of a solid solution in which the solute class 11 chemistry CBSE

Describe the effects of the Second World War class 11 social science CBSE




