Question

Find the area bounded by the curve $y = 2x - {x^2}$, and the line y = x.

Answer 1

Hint – In this particular type of question first draw both the given curves and mark the common region then mark all the intersection points of the curve with the coordinate axes and the intersection points of both the curves then use the concept of area bounded by two curves so use these properties to reach the solution of the question.

Complete step-by-step answer:

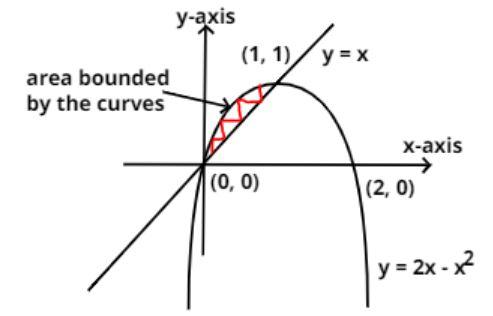
Given curves are
$y = 2x - {x^2}$
This curve is written as
$ \Rightarrow {x^2} - 2x = - y$
Now make the complete square on L.H.S by adding and subtracting the half of the square of the coefficient so we have,
  $ \Rightarrow {x^2} - 2x + {\left( {\dfrac{{ - 2}}{2}} \right)^2} - {\left( {\dfrac{{ - 2}}{2}} \right)^2} = - y$
$ \Rightarrow {x^2} - 2x + 1 - 1 = - y$
$ \Rightarrow {\left( {x - 1} \right)^2} = - \left( {y - 1} \right)$
So as we see this is the equation of the parabola having vertex (1, 1) and opening vertically downwards.
Now the intersection point of this parabola with the x-axis is by putting y = 0 in the equation of the parabola so we have,
$ \Rightarrow {\left( {x - 1} \right)^2} = - \left( {0 - 1} \right) = 1$
Now take square root on the both sides we have,
$ \Rightarrow \left( {x - 1} \right) = \sqrt 1 = \pm 1$
Now when, x – 1 = 1 therefore, x = 2
And when, x – 1 = -1 therefore, x = 0
Now the intersection point of this parabola with the y-axis by putting x = 0 in the equation of the parabola so we have,
$ \Rightarrow {\left( {0 - 1} \right)^2} = - \left( {y - 1} \right)$
$ \Rightarrow 1 = - y + 1$
$ \Rightarrow y = 0$
So the intersection point of the parabola with the coordinate axis is (0, 0) and (2, 0) as shown in the figure.
Now another graph is y = x, as we know this is a straight line passing through origin (0, 0).
Now the intersection of this line with the parabola by substituting y = x in the equation of the parabola so we have,
 $ \Rightarrow x = 2x - {x^2}$
$ \Rightarrow {x^2} - x = 0$
$ \Rightarrow x\left( {x - 1} \right) = 0$
$ \Rightarrow x = 0,1$
As y = x
So the intersection point of the line y = x and the parabola is (0, 0) and (1, 1) as shown in the figure.
So the area bounded by these curves is also shown by the highlighted red color.
Now the limit of x is from 0 to 1.
And the upper curve is parabola and the lower curve is a straight line.
So the area bounded by these curve is given as,
$A = \int\limits_{x = 0}^{x = 1} {\left( {{y_1} - {y_2}} \right)dx} $
Where ${y_1}$ is the upper curve, ${y_1} = 2x - {x^2}$ and ${y_2}$ is the lower curve ${y_2} = x$ so we have,
$ \Rightarrow A = \int\limits_{x = 0}^{x = 1} {\left( {2x - {x^2} - x} \right)dx} $
$ \Rightarrow A = \int\limits_{x = 0}^{x = 1} {\left( {x - {x^2}} \right)dx} $
Now evaluate the integration we have,
$ \Rightarrow A = \left[ {\dfrac{{{x^2}}}{2} - \dfrac{{{x^3}}}{3}} \right]_0^1$
Now apply the lower and upper limits we have,
$ \Rightarrow A = \left[ {\dfrac{1}{2} - \dfrac{1}{3} - 0 + 0} \right]$
Now simplify this we have,
$ \Rightarrow A = \left[ {\dfrac{{3 - 2}}{{2\left( 3 \right)}}} \right] = \dfrac{1}{6}$ square units.
So this is the required area bounded by these two curves.
So this is the required answer.

Note – Whenever we face such types of questions the key concept we have to remember is that the area bounded by the two curves is given as $A = \int\limits_{x = {x_1}}^{x = {x_2}} {\left( {{y_1} - {y_2}} \right)dx} $, where ${y_1}{\text{ and }}{y_2}$are the upper and lower curves in the common region, ${x_1}{\text{ and }}{x_2}$ are the lower and upper limits, so simply substitute the values in this equation as above and integrate it we will get the required answer.