Question

Find the area enclosed by the curve \[x=3\cos t\], \[y=2\sin t\]?

Answer 1

Hint: For the given question we are given a parametric equation and asked to find the area enclosed by the graph. By converting given parametric equations to x and y forms we can see that they will be converted into an eclipse graph as we know that the area of any eclipse graph is 4 times of the symmetrical part. Therefore we can find the area of the graph.

Complete step-by-step answer:
For the given problem we are given to find the area enclosed by the curve \[x=3\cos t\] and \[y=2\sin t\].
Let us consider given 2 equations as equation (1) and equation (2).
\[x=3\cos t....................\left( 1 \right)\]
\[y=2\sin t...................\left( 2 \right)\]
As we know the identity \[{{\cos }^{2}}t+{{\sin }^{2}}t=1\]. So let us consider the identity as (I1).
\[{{\cos }^{2}}t+{{\sin }^{2}}t=1...........\left( I1 \right)\]
Let us find the value of \[\cos t\] and \[\sin t\] from equation (2) and equation (1) respectively.
From equation (1) and equation (2), we get
\[\dfrac{x}{3}=\cos t\] and \[\dfrac{y}{2}=\sin t\].
Let us substitute the above values in identity (I1), we get
\[\Rightarrow {{\left( \dfrac{x}{3} \right)}^{2}}+{{\left( \dfrac{y}{2} \right)}^{2}}=1\]
Let us consider the above equation as equation (3).
\[\Rightarrow {{\left( \dfrac{x}{3} \right)}^{2}}+{{\left( \dfrac{y}{2} \right)}^{2}}=1.......................\left( 3 \right)\]
Let us plot the graph for the above equation

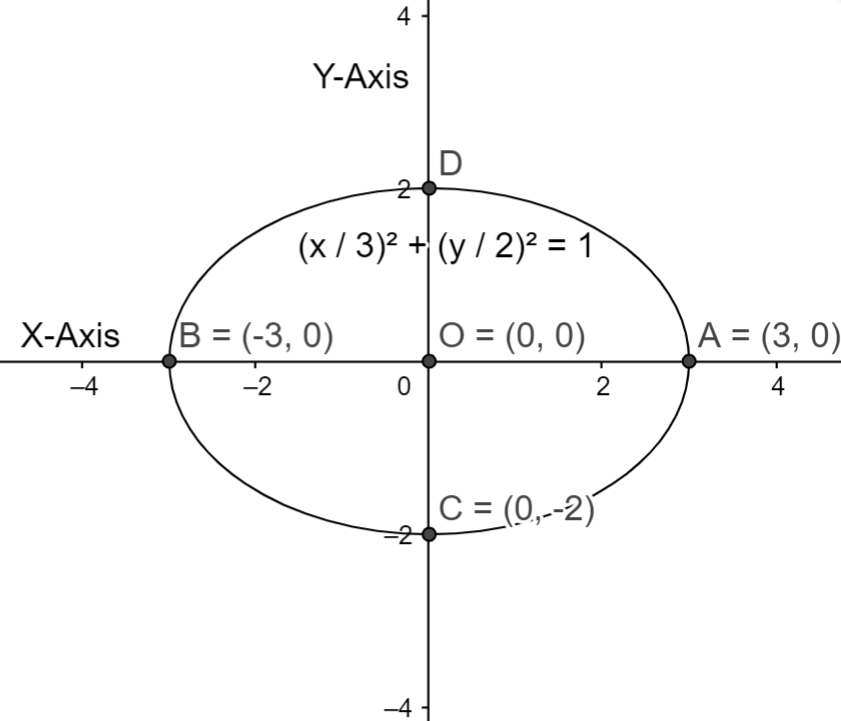
As we know the equation of eclipse is in the form \[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\]. So, as we know that the graph is symmetrically partitioned by 4 parts. Therefore, by finding the one part we can find the total area of the graph.
\[\Rightarrow \text{Area=4}\text{.Area of OAB}\]
\[=4\int\limits_{0}^{3}{ydx}\]
Let us consider the above equation as equation (4).
\[A=4\int\limits_{0}^{3}{ydx}...................\left( 4 \right)\]
Therefore, from the equation (1) we get
\[\Rightarrow y=\left( \dfrac{2}{3}\sqrt{\left( 9-{{x}^{2}} \right)} \right)\]
Let us substitute the above value in equation (4) we get,
\[\Rightarrow A=4\int\limits_{0}^{3}{\left( \dfrac{2}{3}\sqrt{\left( 9-{{x}^{2}} \right)} \right)dx}\]
\[\Rightarrow A=\dfrac{8}{3}\int\limits_{0}^{3}{\left( \sqrt{\left( {{3}^{2}}-{{x}^{2}} \right)} \right)dx}\]
Let us consider above equation as equation (5).
\[\Rightarrow A=\dfrac{8}{3}\int\limits_{0}^{3}{\left( \sqrt{\left( {{3}^{2}}-{{x}^{2}} \right)} \right)dx}.........\left( 5 \right)\]
By the formula \[\int{{{a}^{2}}-{{x}^{2}}dx=\left| \dfrac{x}{2}\sqrt{{{a}^{2}}-{{x}^{2}}}+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\dfrac{x}{a} \right|}\]
By applying the formula to the equation (5), we get
\[\Rightarrow A=\dfrac{8}{3}\left| \dfrac{x}{2}\sqrt{{{3}^{2}}-{{x}^{2}}}+\dfrac{9}{2}{{\sin }^{-1}}\dfrac{x}{3} \right|_{0}^{3}\]
\[\Rightarrow A=\dfrac{8}{3}\left| \dfrac{9}{2}{{\sin }^{-1}}\left( \sin \dfrac{\pi }{2} \right) \right|\]
\[\Rightarrow A=6\pi squnits\]
Therefore, the area of the given graph is \[6\pi squints\].

Note: While doing this problem we have to remember a point that we have to convert the given parametric equation to the geometric equation to get the graph. We should be aware of all integration formulas to solve this question