
Find the area enclosed by the given figure
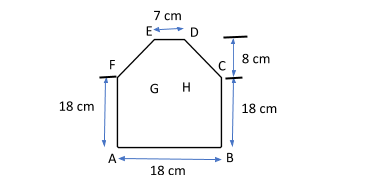

Answer
477k+ views
Hint: To find the area enclosed in the given figure split the figure as shown below:
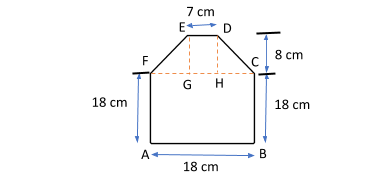
This figure is into four parts:
A large square, ABCF whose side is equal to 18 cm.
A rectangle, DEGH whose length and breath are equal to 7cm and 8cm respectively.
Two right angle triangles, $\vartriangle CDH\& \vartriangle EFG$ whose height is 8cm.
To obtain the total area, find out the area of each part then by adding all we get the total area.
Complete step-by-step answer:
The total area enclosed of the figure can be obtained by adding the area enclosed by a square, a rectangle and two triangles. We get,
$ \Rightarrow {A_{TL}} = {A_S} + {A_R} + {A_{{T_1}}} + {A_{{T_2}}}$ ……(3)
Where${A_{TL}}$is the total area enclosed by the figure,
${A_S}$is the area enclosed by the square ABCF,
${A_R}$ is the area enclosed by the rectangle DEGH,
${A_{{T_1}}}$is the area enclosed by the triangle 1 i.e.$\vartriangle CDH$&
${A_{{T_2}}}$is the area enclosed by the triangle 2 i.e.$\vartriangle EFG$.
Now step by step find the area of each as follows:
Area of the square= $ = side \times side$
Here, side $ = 18cm$
Hence, area of square$ = 18 \times 18 = 324c{m^2}$
$ \Rightarrow {A_S} = 324c{m^2}$ ……..(2)
Area of the rectangle $ = l \times b$
Here, $l = 7cm\& b = 8cm$
Hence area of the rectangle$ = 7 \times 8 = 56c{m^2}$
$ \Rightarrow {A_R} = 56c{m^2}$ ………(3)
Area of triangle$ = \dfrac{1}{2} \times base \times height$
As we don’t know the base, firstly we will find the value of base of both the triangles as follow:
$FG + CH = FC - GH = 18 - 7 = 11cm$
$
\Rightarrow {A_{{T_1}}} = \dfrac{1}{2} \times CH \times height = \dfrac{1}{2} \times CH \times 8 = 4CH \\
\Rightarrow {A_{{T_2}}} = \dfrac{1}{2} \times FG \times height = \dfrac{1}{2} \times FG \times 8 = 4FG \\
\Rightarrow {A_{{T_1}}} + {A_{{T_2}}} = 4CH + 4FG = 4(CH + FG) = 4 \times 11 = 44c{m^2} \\
$
$ \Rightarrow {A_{{T_1}}} + {A_{{T_2}}} = 44c{m^2}$ ……..(4)
From (1), (2), (3) & (4)
$
\Rightarrow {A_{TL}} = 324 + 56 + 44 \\
\Rightarrow {A_{TL}} = 424c{m^2} \\
$
Hence the total area enclosed by the given figure is $424c{m^2}$.
Note: Some students get confused in solving these types of questions and leave the question. As they see the figure and think how to find the area as they have no formula for that. So, first of all you should imagine how many geometric figures it can have. Now split the figure and find the area of each figure. While splitting the figures you should split the figure in this way that you could find the area of each including in the given figure. You should cover the whole figure otherwise it may get wrong.

This figure is into four parts:
A large square, ABCF whose side is equal to 18 cm.
A rectangle, DEGH whose length and breath are equal to 7cm and 8cm respectively.
Two right angle triangles, $\vartriangle CDH\& \vartriangle EFG$ whose height is 8cm.
To obtain the total area, find out the area of each part then by adding all we get the total area.
Complete step-by-step answer:
The total area enclosed of the figure can be obtained by adding the area enclosed by a square, a rectangle and two triangles. We get,
$ \Rightarrow {A_{TL}} = {A_S} + {A_R} + {A_{{T_1}}} + {A_{{T_2}}}$ ……(3)
Where${A_{TL}}$is the total area enclosed by the figure,
${A_S}$is the area enclosed by the square ABCF,
${A_R}$ is the area enclosed by the rectangle DEGH,
${A_{{T_1}}}$is the area enclosed by the triangle 1 i.e.$\vartriangle CDH$&
${A_{{T_2}}}$is the area enclosed by the triangle 2 i.e.$\vartriangle EFG$.
Now step by step find the area of each as follows:
Area of the square= $ = side \times side$
Here, side $ = 18cm$
Hence, area of square$ = 18 \times 18 = 324c{m^2}$
$ \Rightarrow {A_S} = 324c{m^2}$ ……..(2)
Area of the rectangle $ = l \times b$
Here, $l = 7cm\& b = 8cm$
Hence area of the rectangle$ = 7 \times 8 = 56c{m^2}$
$ \Rightarrow {A_R} = 56c{m^2}$ ………(3)
Area of triangle$ = \dfrac{1}{2} \times base \times height$
As we don’t know the base, firstly we will find the value of base of both the triangles as follow:
$FG + CH = FC - GH = 18 - 7 = 11cm$
$
\Rightarrow {A_{{T_1}}} = \dfrac{1}{2} \times CH \times height = \dfrac{1}{2} \times CH \times 8 = 4CH \\
\Rightarrow {A_{{T_2}}} = \dfrac{1}{2} \times FG \times height = \dfrac{1}{2} \times FG \times 8 = 4FG \\
\Rightarrow {A_{{T_1}}} + {A_{{T_2}}} = 4CH + 4FG = 4(CH + FG) = 4 \times 11 = 44c{m^2} \\
$
$ \Rightarrow {A_{{T_1}}} + {A_{{T_2}}} = 44c{m^2}$ ……..(4)
From (1), (2), (3) & (4)
$
\Rightarrow {A_{TL}} = 324 + 56 + 44 \\
\Rightarrow {A_{TL}} = 424c{m^2} \\
$
Hence the total area enclosed by the given figure is $424c{m^2}$.
Note: Some students get confused in solving these types of questions and leave the question. As they see the figure and think how to find the area as they have no formula for that. So, first of all you should imagine how many geometric figures it can have. Now split the figure and find the area of each figure. While splitting the figures you should split the figure in this way that you could find the area of each including in the given figure. You should cover the whole figure otherwise it may get wrong.
Recently Updated Pages
Glucose when reduced with HI and red Phosphorus gives class 11 chemistry CBSE

The highest possible oxidation states of Uranium and class 11 chemistry CBSE

Find the value of x if the mode of the following data class 11 maths CBSE

Which of the following can be used in the Friedel Crafts class 11 chemistry CBSE

A sphere of mass 40 kg is attracted by a second sphere class 11 physics CBSE

Statement I Reactivity of aluminium decreases when class 11 chemistry CBSE

Trending doubts
When people say No pun intended what does that mea class 8 english CBSE

In Indian rupees 1 trillion is equal to how many c class 8 maths CBSE

How many ounces are in 500 mL class 8 maths CBSE

Which king started the organization of the Kumbh fair class 8 social science CBSE

What is BLO What is the full form of BLO class 8 social science CBSE

Advantages and disadvantages of science




