Question

Find the area of a regular octagon of side
a) 4 cm
b) 5 cm

Answer 1

Hint: For solving the given problem, we should know about the basics of octagon and a regular figure. The area of a regular octagon is given by $2{{a}^{2}}(1+\sqrt{2})$. Here is the length of the side of an octagon. We use this formula to find the area of the regular octagon for sides 4 and 5 cm.

Complete step-by-step answer:

Before solving the problem, let’s know about some of the basics of a regular octagon. Octagon is a convex polygon (all diagonals intersect inside the figure and all the internal angles are less than 180 degrees) which has 8 sides. In the above problem, we are given that it is a regular octagon, this means that all the sides of the octagon are equal and all the angles of the octagon are equal. Below, we have the figure of a regular octagon. We have,

As can be seen from the above figure, we only have to show the side length of one side of this octagon since all other sides are equal. Now, coming back to the problem, we have two subparts-

(a) Area for 4 cm
The formula for the area of a regular octagon is given by $2{{a}^{2}}(1+\sqrt{2})$. Here, a is the side length of the regular octagon. Thus,
Area = $2{{a}^{2}}(1+\sqrt{2})$
Area = $2\times {{4}^{2}}(1+\sqrt{2})$
Area =$77.255\text{ c}{{\text{m}}^{2}}$
(b) Area for 5 cm
Again using the formula of the area of the regular octagon, which is given by $2{{a}^{2}}(1+\sqrt{2})$. Here, a is the side length of the regular octagon. Thus,
Area = $2{{a}^{2}}(1+\sqrt{2})$
Area = $2\times {{5}^{2}}(1+\sqrt{2})$
Area = $120.71\text{ c}{{\text{m}}^{2}}$

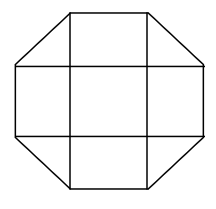
Note: The formula for the area of an octagon can always be found by dividing the figure into portions of polygons whose area is well known. To illustrate, in the figure below we have divided the octagon into rectangles and right triangles whose area is easy to find. We only have to make use of basic geometry to find lengths and breadths of these figures and then find the sum of them to get the area of the octagon.