Question

Find the area of a sector with a central angle of 120 degrees and a radius of 10 cm.
A) $10\pi {\text{ }}\mathop {cm}\nolimits^2 $
B) $20\pi {\text{ }}\mathop {cm}\nolimits^2 $
C) $30\pi {\text{ }}\mathop {cm}\nolimits^2 $
D) $40\pi {\text{ }}\mathop {cm}\nolimits^2 $

Answer 1

Hint: We know that the portion (or part) of the circular region enclosed by two radii and the corresponding arc is called a sector of the circle.

Figure: Sectors of the circle
Use the unitary method to calculate the Area of the sector of the circle.

Complete step-by-step answer:
Step 1: Draw the given circle.

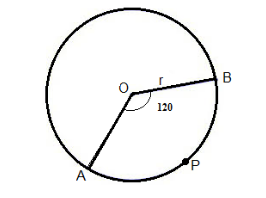
Figure: Given circle with center O
Step 2: Given that:
The radius of the given circle with center O = 10 cm
Let radius denoted by r.
$ \Rightarrow r = {\text{OB}} = {\text{OA}} = 10{\text{ cm}}$
The angle subtended by the chord at the center:
I.e. $\angle AOB = 120^\circ $
Let, $\theta = \angle AOB = 120^\circ $
Step 3: Calculate the area of the sector (OBPA)
Area of circle (or a disk) \[ = \pi \mathop r\nolimits^2 \]sq. units
The circular region to be a sector forming an angle of $360^\circ $at the center.
Let’s find the area OBPA using the unitary method.
When the angle at the center is $360^\circ $, area of the sector \[ = \pi \mathop r\nolimits^2 \]
So, when the angle at the center is $1^\circ $, area of the sector \[ = \dfrac{{\pi \mathop r\nolimits^2 }}{{360^\circ }}\]
Therefore, when the angle at the center is $\theta $, area of the sector = $\dfrac{\theta }{{{{360}^ \circ }}} \times \pi \mathop r\nolimits^2 \;$
$\because \theta = 120^\circ $
Radius, r = 10 cm
Thus the area of the sector formed by radius when the angle at the center is $120^\circ $$ = \dfrac{{120^\circ }}{{360^\circ }} \times \pi \mathop {\left( {10} \right)}\nolimits^2 $
$
   \Rightarrow \dfrac{{120^\circ }}{{360^\circ }} \times \pi \times 10 \times 10 \\
   \Rightarrow \dfrac{{100\pi }}{3} \\
   \Rightarrow 33.33{\text{ }}\pi \mathop {cm}\nolimits^2 \\
 $
The area of a sector with a central angle of 120 degrees and a radius of 10 cm is \[33.33\pi \mathop {cm}\nolimits^2 \simeq 30\pi \mathop {cm}\nolimits^2 \].

Thus the correct option is (C).

Note: The result, ‘when the angle at the center is $\theta $, area of the sector = $\dfrac{\theta }{{{{360}^ \circ }}} \times \pi \mathop r\nolimits^2 \;$ sq. units’ can be directly used to find the area of a sector of a circle with radius, r.
Keep in mind that the portion (or part) of the circular region enclosed between a chord and the corresponding arc is called a segment of the circle.

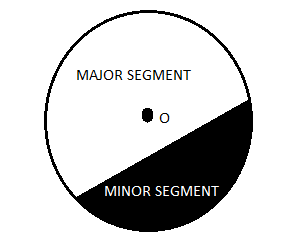
Figure: Segments of Circle
When we write ‘segment’ and ‘sector’ we will mean the ‘minor segment’ and the ‘minor sector’ respectively unless stated otherwise.
The perimeter of circle $ = 2\pi r$units.