
Find the area of a square, if the measure of its each diagonal is
Answer
424.2k+ views
Hint: In this problem we need to calculate the area of the square with a given diagonal length. First we will assume the side length of the square as
Complete step-by-step solution:
Given that, the diagonal length of the square is
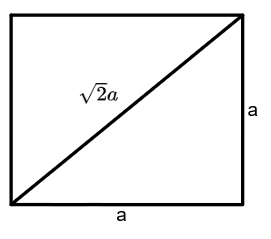
Let us assume the side length of the square as
In the problem we have given that the diagonal length is
Dividing the above equation with
Now we have the side length of the square
We know that the area of the square with the side length
Now the area of the square of having side length
Simplifying the above equation by using basic mathematical operations, then we will have
Hence the area of the square with diagonal length
Note: For this problem we need not to calculate the side length of the square to find the area of the square. We have the formula for the area of the square with a given diagonal length
Complete step-by-step solution:
Given that, the diagonal length of the square is

Let us assume the side length of the square as
In the problem we have given that the diagonal length is
Dividing the above equation with
Now we have the side length of the square
We know that the area of the square with the side length
Now the area of the square of having side length
Simplifying the above equation by using basic mathematical operations, then we will have
Hence the area of the square with diagonal length
Note: For this problem we need not to calculate the side length of the square to find the area of the square. We have the formula for the area of the square with a given diagonal length
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
EMI starts from ₹3,487.34 per month
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
How many ounces are in 500 mL class 8 maths CBSE

Summary of the poem Where the Mind is Without Fear class 8 english CBSE

Advantages and disadvantages of science

10 slogans on organ donation class 8 english CBSE

The LCM and HCF of two rational numbers are equal Then class 8 maths CBSE

In Indian rupees 1 trillion is equal to how many c class 8 maths CBSE





