Question

Find the area of four walls of a room (assume that there are no doors or windows) if its length is 12m, breadth 10m and height 7.5m.

Answer 1

Hint: In this question, we are given the length, the breadth and the height of the room. We need to find the area of four walls of the room. For this, we will find areas of individual rectangles that walls of room represent and then add them to get the total area. Area of the rectangle having length 'l' and breadth 'b' is given by $A=l\times b$.

Complete step-by-step answer:
Here we are given the length of the room as 12m.
The breadth of the room is 10m and
The height of the room is 7.5m.
Our room will be in the shape of a cuboid having walls as the shape of a rectangle.
Cuboid looks like this:

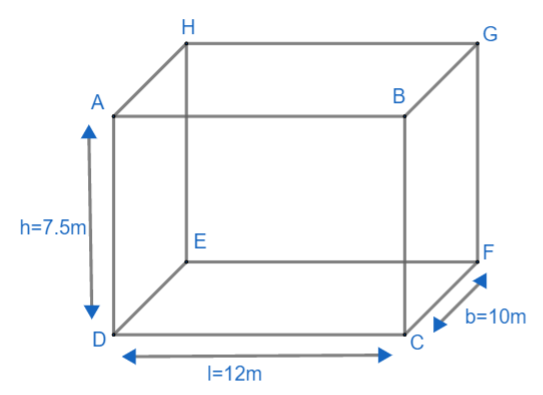
We need to find the area of four walls, which means we need to find the area of four rectangles ABCD, EFGH, ADEH and BCFG.
Let us calculate areas of the rectangle. Area of the rectangle having length and breadth is given by $A=l\times b$.
For ABCD, we have length as 12m and height as 7.5m. So,
Area becomes equal to $\Rightarrow \left( 12\times 7.5 \right){{m}^{2}}=90{{m}^{2}}$.
Similarly for EFGH, we have length as 12m and height as 7.5m. So,
Area becomes equal to $\Rightarrow \left( 12\times 7.5 \right){{m}^{2}}=90{{m}^{2}}$.
For ADEH, we have breadth as 10m and height as 7.5m. So,
Area becomes equal to $\Rightarrow \left( 10\times 7.5 \right){{m}^{2}}=75{{m}^{2}}$.
Similarly for BCFG, we have breadth as 10m and height as 7.5m. So,
Area becomes equal to $\Rightarrow \left( 10\times 7.5 \right){{m}^{2}}=75{{m}^{2}}$.
Now the area of all four walls will be equal to the sum of rectangle ABCD, EFGH, ADEH and BCFG. So we get:
Area of four walls $\Rightarrow \left( 90+90+75+75 \right){{m}^{2}}=330{{m}^{2}}$.
Hence the required area of the wall is $330{{m}^{2}}$.

Note: Students often make the mistake of getting confused between height and length. Take care of units while finding the area. Squared units are used for area. Here all measurements were in meters so we have used squared meters for area. Students can directly learn the formula of finding the area of cuboid excluding base and top as $2\left( lh+bh \right)$.