Question

Find the area of the house drawing given in the figure.

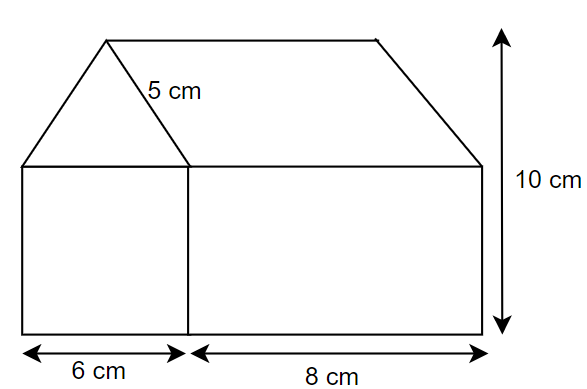
Answer 1

Hint: The basic method to solve such a question of area and perimeter is to find the area of an unknown figure by dividing the bigger shape into small shapes of known structure, for which we can easily calculate the area and perimeter. So, we will do the same here in the question and then as the first step, we will name the figure and then find the small known figures. Finally, we will add all the smaller areas to get the area of the entire figure and so get our desired answer.

Complete step-by-step solution:
In this question, we have been asked to find the area of the given figure of a house. To do so, we will first divide the house into smaller figures and name them. So, let us consider the entire shape as given below,

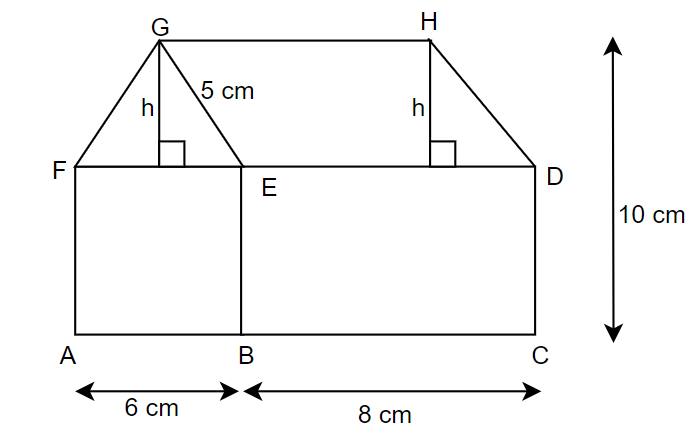
Here, we can see that the entire figure can be divided into 4 parts, namely a square, a parallelogram, a rectangle and a triangle. So, we have the following as,
ABEF is a square.
EBCD is a rectangle.
EDHG is a parallelogram.
FEG is a triangle.
So, we will have the area of the house = area of ABEF + area of EBCD + area of EDHG + area of FEG.
We will now find the areas one by one.
The area of ABEF, which is a square is given as,
Area of ABEF = $\text{sid}{{\text{e}}^{2}}$.
Since ABEF is a square, and AB = 6cm. So, AF = 6cm, FE = 6cm, EB = 6cm.
So, we get the area of ABEF = ${{\left( 6 \right)}^{2}}\Rightarrow 36c{{m}^{2}}$.
The area of EBCD, which is a rectangle is given as,
Area of EBCD = length $\times $ breadth.
Since ABEF is a rectangle, and BC = ED and EB = CD. So, ED = 6cm, CD = 8cm.
So, we get the area of ABEF = BC $\times $ EB $\Rightarrow 8\times 6\Rightarrow 48c{{m}^{2}}$.
 Now, let us assume a perpendicular from G and H to FE and Ed respectively. Since they originate from the same line and fall on the same straight line, they are equal in length. Let us say they are equal to h.
Now, the total height of the house = CD + h
$\begin{align}
  & \Rightarrow 10cm=6cm+h \\
 & \Rightarrow h=4cm \\
\end{align}$
Now, the area of the parallelogram EDHG is given as,
Area of EDHG = base $\times $ height.
So, area = ED $\times $ h $\Rightarrow 8\times 4\Rightarrow 32c{{m}^{2}}$
Now, we know the area of a triangle FGE is given as,
Area of FGE = $\dfrac{1}{2}$ $\times $ base $\times $ height.
So, area of FGE = $\dfrac{1}{2}$ $\times $ FE $\times $ h $\Rightarrow \dfrac{1}{2}\times 6\times 4\Rightarrow 12c{{m}^{2}}$
Now we will add all these areas to get the area of the house. So, the area of the house is,
$36c{{m}^{2}}+48c{{m}^{2}}+32c{{m}^{2}}+12c{{m}^{2}}=128c{{m}^{2}}$
Therefore, we get the area of the house is $128c{{m}^{2}}$.

Note: The major mistake that is seen in this type of questions is with the formula of all these figures and the fact that we need to make sure that the small figures we distribute the bigger picture in, we have to make sure that we can find the areas of those figures properly.