Question

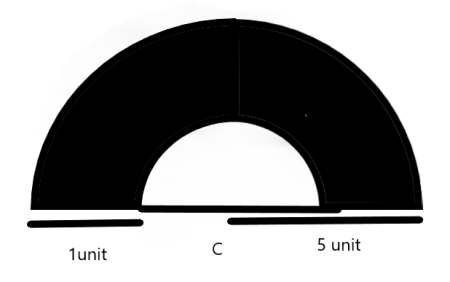
Find the area of the shaded portion

A) \[{\text{7}}{\text{.5$\pi$ sq}}{\text{.unit}}\]
B) \[{\text{6}}{\text{.5$\pi$ sq}}{\text{.unit}}\]
C) \[{\text{5}}{\text{.5$\pi$ sq}}{\text{.unit}}\]
D) \[{\text{4}}{\text{.5$\pi$ sq}}{\text{.unit}}\]

Answer 1

Hint: As we can see that the given figure is of concentric semi-circle. So, in order to calculate the area of the shaded portion subtract area of outer semicircle with the area of inner semicircle. Area of semicircle is given by \[\dfrac{{{\text{$\pi$ }}{{\text{r}}^{\text{2}}}}}{{\text{2}}}\].

Complete step by step answer:

As given that the radius of the outer circle is \[{\text{5unit}}\]and difference between the radius of both the circle is \[{\text{1unit}}\]
So forming the equation among the given and solving it,
\[
  {\text{R = 5}} \\
  {\text{R - r = 1}} \\
  {\text{so,r = 4unit}} \\
 \]
Now , calculating area of both the semi circles so they are
Area of semicircle is \[\dfrac{{{\text{$\pi$ }}{{\text{r}}^{\text{2}}}}}{2}\]
\[
  {\text{A = }}\dfrac{{{\text{$\pi$ }}{{\text{R}}^{\text{2}}}}}{{\text{2}}}{\text{ = }}\dfrac{{{\text{$\pi$ }}{{\text{5}}^{\text{2}}}}}{{\text{2}}}{\text{ = 12}}{\text{.5$\pi$ sq}}{\text{.unit}} \\
  {\text{A' = }}\dfrac{{{\text{$\pi$ }}{{\text{r}}^{\text{2}}}}}{{\text{2}}}{\text{ = }}\dfrac{{{\text{$\pi$ }}{{\text{4}}^{\text{2}}}}}{{\text{2}}}{\text{ = 8$\pi$ sq}}{\text{.unit}} \\
 \]
Now , as we required the area of shaded portion so it will be given by
\[
  {\text{ = A - A'}} \\
  {\text{ = 12}}{\text{.5$\pi$ - 8$\pi$ }} \\
  {\text{ = 4}}{\text{.5$\pi$ sq}}{\text{.unit}} \\
 \]
Hence, option (d) is our correct answer.

Note: Here we don’t need to substitute the value of \[\pi \], as in options we have area w.r.t \[\pi \]. A circle is a shape consisting of all points in a plane that are a given distance from a given point, the center; equivalently it is the curve traced out by a point that moves in a plane so that its distance from a given point is constant. In geometry, a semicircle is a one-dimensional locus of points that forms half of a circle. The area of a semicircle is half of the circle.