Question

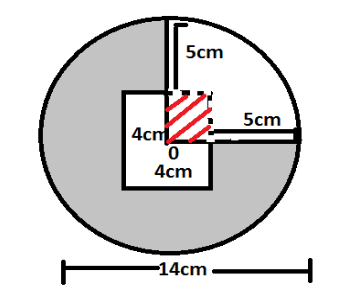
Find the area of the shaded region in the following figure:-

A. 28.45 sq. cm
B. 113.6 sq. cm
C. 59.8 sq. cm
D. 46.88 sq. cm

Answer 1

Hint: In such questions we need to analyze the different shapes which make up the shaded region and calculate the area accordingly, for this question we need the area of the circle square and quadrant to calculate the area of the shaded region.

Complete Step-by-Step solution:
Given,
Diameter of circle= 14cm
Radius of circle=7cm
Side of square=4cm
Angle of quadrant=\[\dfrac{\pi }{2}\]
Area of circle=\[\pi {r^2}\]
\[
   = (\dfrac{{22}}{7}) \times {(7)^2} \\
   = 154c{m^2} \\
\]
Now we need to calculate the area of the square as well as quadrant.
Area of square\[ = {(side)^2}\]
\[ = {(4)^2}\]=16\[c{m^2}\]
Area of quadrant=\[\dfrac{1}{4}\pi {r^2}\]
\[
   = \dfrac{1}{4} \times (\dfrac{{22}}{7}) \times {(7)^2} \\
   = 38.5c{m^2} \\
\]
Now we need to analyze the shaded region carefully,
Area of shaded region=area of circle-area of square-area of quadrant + area of square of side 2cm
We need to add the area of square of side 2cm as in subtracting area of quadrant and area of square of side 4cm; we subtract the area of square of side 2cm twice.
Area of square of side 2cm\[ = {(side)^2}\]
\[
   = {(2)^2} \\
   = 4c{m^2} \\
\]
Area of shaded region=area of circle-area of square-area of quadrant + area of square of side 2cm
=154-16-38.5+4
=103.5 \[c{m^2}\]
Hence, the answer to this question is 103.5 \[c{m^2}\].

Note: In such types of questions we need to take care of which area to be subtracted and which ones to be added and also take care of not adding or subtracting areas not more than once, also we need to remember basic formulae of area of figures in a plane.