
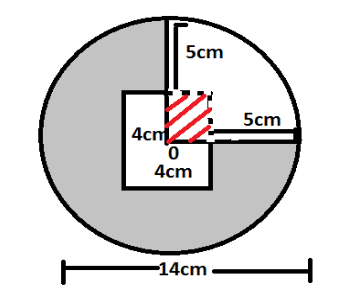
Find the area of the shaded region in the following figure:-
A. 28.45 sq. cm
B. 113.6 sq. cm
C. 59.8 sq. cm
D. 46.88 sq. cm

Answer
501.9k+ views
Hint: In such questions we need to analyze the different shapes which make up the shaded region and calculate the area accordingly, for this question we need the area of the circle square and quadrant to calculate the area of the shaded region.
Complete Step-by-Step solution:
Given,
Diameter of circle= 14cm
Radius of circle=7cm
Side of square=4cm
Angle of quadrant=\[\dfrac{\pi }{2}\]
Area of circle=\[\pi {r^2}\]
\[
= (\dfrac{{22}}{7}) \times {(7)^2} \\
= 154c{m^2} \\
\]
Now we need to calculate the area of the square as well as quadrant.
Area of square\[ = {(side)^2}\]
\[ = {(4)^2}\]=16\[c{m^2}\]
Area of quadrant=\[\dfrac{1}{4}\pi {r^2}\]
\[
= \dfrac{1}{4} \times (\dfrac{{22}}{7}) \times {(7)^2} \\
= 38.5c{m^2} \\
\]
Now we need to analyze the shaded region carefully,
Area of shaded region=area of circle-area of square-area of quadrant + area of square of side 2cm
We need to add the area of square of side 2cm as in subtracting area of quadrant and area of square of side 4cm; we subtract the area of square of side 2cm twice.
Area of square of side 2cm\[ = {(side)^2}\]
\[
= {(2)^2} \\
= 4c{m^2} \\
\]
Area of shaded region=area of circle-area of square-area of quadrant + area of square of side 2cm
=154-16-38.5+4
=103.5 \[c{m^2}\]
Hence, the answer to this question is 103.5 \[c{m^2}\].
Note: In such types of questions we need to take care of which area to be subtracted and which ones to be added and also take care of not adding or subtracting areas not more than once, also we need to remember basic formulae of area of figures in a plane.
Complete Step-by-Step solution:
Given,
Diameter of circle= 14cm
Radius of circle=7cm
Side of square=4cm
Angle of quadrant=\[\dfrac{\pi }{2}\]
Area of circle=\[\pi {r^2}\]
\[
= (\dfrac{{22}}{7}) \times {(7)^2} \\
= 154c{m^2} \\
\]
Now we need to calculate the area of the square as well as quadrant.
Area of square\[ = {(side)^2}\]
\[ = {(4)^2}\]=16\[c{m^2}\]
Area of quadrant=\[\dfrac{1}{4}\pi {r^2}\]
\[
= \dfrac{1}{4} \times (\dfrac{{22}}{7}) \times {(7)^2} \\
= 38.5c{m^2} \\
\]
Now we need to analyze the shaded region carefully,
Area of shaded region=area of circle-area of square-area of quadrant + area of square of side 2cm
We need to add the area of square of side 2cm as in subtracting area of quadrant and area of square of side 4cm; we subtract the area of square of side 2cm twice.
Area of square of side 2cm\[ = {(side)^2}\]
\[
= {(2)^2} \\
= 4c{m^2} \\
\]
Area of shaded region=area of circle-area of square-area of quadrant + area of square of side 2cm
=154-16-38.5+4
=103.5 \[c{m^2}\]
Hence, the answer to this question is 103.5 \[c{m^2}\].
Note: In such types of questions we need to take care of which area to be subtracted and which ones to be added and also take care of not adding or subtracting areas not more than once, also we need to remember basic formulae of area of figures in a plane.
Recently Updated Pages
What percentage of the area in India is covered by class 10 social science CBSE

The area of a 6m wide road outside a garden in all class 10 maths CBSE

What is the electric flux through a cube of side 1 class 10 physics CBSE

If one root of x2 x k 0 maybe the square of the other class 10 maths CBSE

The radius and height of a cylinder are in the ratio class 10 maths CBSE

An almirah is sold for 5400 Rs after allowing a discount class 10 maths CBSE

Trending doubts
The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Why is there a time difference of about 5 hours between class 10 social science CBSE

Who was Subhash Chandra Bose Why was he called Net class 10 english CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

Explain the Treaty of Vienna of 1815 class 10 social science CBSE




