
Find the capacitive time constant of the RC circuit shown in the figure.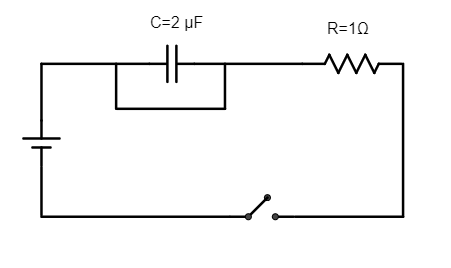
a) $0$
b) $\infty $
c) $2{\text{s}}$
d) $2\mu {\text{s}}$
Answer
122.1k+ views
Hint: The capacitor is shorted in the circuit diagram. This suggests that the potential difference across the capacitor is zero.
Formula Used: Time constant of the circuit is $\tau = RC$
Complete step by step answer:
Step 1: Explain the circuit diagram.
Step 2: Determine the time constant of the circuit.
Additional Information: When an increasing DC voltage is applied to a discharged capacitor, the capacitor charges up. When the voltage decreases the capacitor again discharges. This charging and discharging of the capacitor energy never happens in an instant. It takes some amount of time for the capacitor to charge or discharge to a specific percentage of its maximum supply value. This time is known as the time constant $\tau $. If the capacitor in the above RC circuit was not shorted, then the capacitor would have gradually charged up through the resistor until the voltage across the plates reached the supply voltage.
Note: Time constant represents the speed at which a system responds to change. Or, in this case it represents how fast the capacitor charges through the resistor. Here, the time constant is infinity. This means that the capacitor does not charge at all.
Formula Used: Time constant of the circuit is $\tau = RC$
Complete step by step answer:
Step 1: Explain the circuit diagram.
A capacitor of $C = 2\mu {\text{F}}$ is connected in series with a resistor of resistance $R = 1\Omega $ and connected to a battery. The capacitor is shorted.
Step 2: Determine the time constant of the circuit.
Time constant of the circuit is given by $\tau = RC$ .
Since the capacitor is shorted, the potential difference between the two plates will be zero.
We know that $C = \dfrac{Q}{V}$ .
Now, potential difference $V = 0$ .
This implies that $C = \infty $ .
Hence $\tau = R \times \infty = \infty $ .
Therefore, the correct option is b)$\infty $ .
Additional Information: When an increasing DC voltage is applied to a discharged capacitor, the capacitor charges up. When the voltage decreases the capacitor again discharges. This charging and discharging of the capacitor energy never happens in an instant. It takes some amount of time for the capacitor to charge or discharge to a specific percentage of its maximum supply value. This time is known as the time constant $\tau $. If the capacitor in the above RC circuit was not shorted, then the capacitor would have gradually charged up through the resistor until the voltage across the plates reached the supply voltage.
Note: Time constant represents the speed at which a system responds to change. Or, in this case it represents how fast the capacitor charges through the resistor. Here, the time constant is infinity. This means that the capacitor does not charge at all.
Recently Updated Pages
How to find Oxidation Number - Important Concepts for JEE

How Electromagnetic Waves are Formed - Important Concepts for JEE

Electrical Resistance - Important Concepts and Tips for JEE

Average Atomic Mass - Important Concepts and Tips for JEE

Chemical Equation - Important Concepts and Tips for JEE

Concept of CP and CV of Gas - Important Concepts and Tips for JEE

Trending doubts
JEE Mains 2025: Check Important Dates, Syllabus, Exam Pattern, Fee and Updates

JEE Main Login 2045: Step-by-Step Instructions and Details

JEE Main Chemistry Question Paper with Answer Keys and Solutions

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Keys & Solutions

JEE Main Chemistry Exam Pattern 2025

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

JEE Advanced 2025: Dates, Registration, Syllabus, Eligibility Criteria and More

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

JEE Main 2025: Conversion of Galvanometer Into Ammeter And Voltmeter in Physics

Dual Nature of Radiation and Matter Class 12 Notes: CBSE Physics Chapter 11

Electric field due to uniformly charged sphere class 12 physics JEE_Main




