
How do you find the center and radius of the circle \[4{{x}^{2}}-16x+4{{y}^{2}}-24y+36=0\]?
Answer
536.4k+ views
Hint: The general form of the equation of circle is \[{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\]. We can see that coefficients of the square terms are one in the above equation. In the given equation, this condition is not followed, so we have to make the coefficients one. We can find the coordinates of the center of the circle and the radius using the values of the coefficient of the equation. The coordinate of the center of the circle are \[\left( -g,-f \right)\]. The radius of the circle is \[\sqrt{{{g}^{2}}+{{f}^{2}}-c}\]. To find the values of the coefficient, we need to compare the given equation with the general form of the equation of circle.
Complete step by step solution:
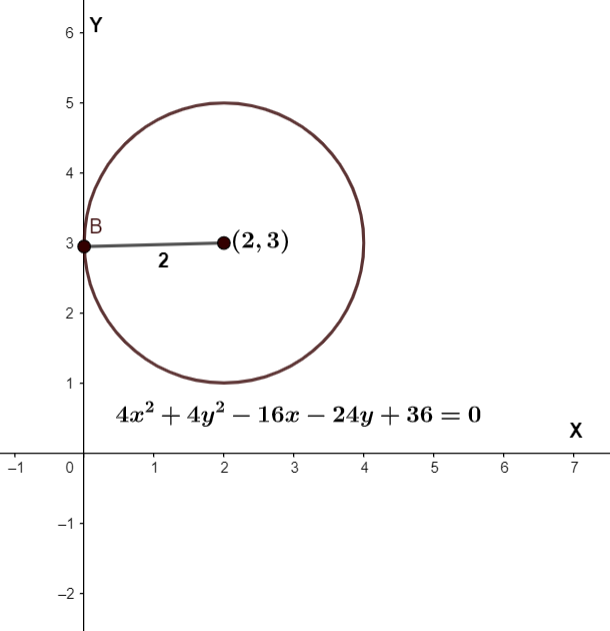
We are given the equation of the circle \[4{{x}^{2}}-16x+4{{y}^{2}}-24y+36=0\].
Dividing both sides of the equation by 4, we get \[{{x}^{2}}-4x+{{y}^{2}}-6y+9=0\]. We need to find its center and radius. Comparing the given equation with the general form of the equation of the circle. We get the values of g, f, and c as \[-2,-3\And 9\] respectively. We know that for a circle represented by the general form of the equation, the X and Y coordinates of the center are \[-g,-f\] respectively. Thus, for the given circle, by substituting the values of g and f, we get the coordinates of the center as \[\left( -(-2),-(-3) \right)\]. Simplifying this, we get center coordinates \[\left( 2,3 \right)\].
The radius of the circle is \[\sqrt{{{g}^{2}}+{{f}^{2}}-c}\], substituting the values of g, f, and c, we get radius as\[\sqrt{{{2}^{2}}+{{3}^{2}}-9}=2\].
The graph of the circle is as follows,
Note: We should remember for an equation of conic of form \[a{{x}^{2}}+b{{y}^{2}}+2gx+2fy+2hxy+c=0\] it must follow the following conditions to represent a circle. The first condition is \[a=b\]. The second condition is that \[h\] must be zero.
Complete step by step solution:
We are given the equation of the circle \[4{{x}^{2}}-16x+4{{y}^{2}}-24y+36=0\].
Dividing both sides of the equation by 4, we get \[{{x}^{2}}-4x+{{y}^{2}}-6y+9=0\]. We need to find its center and radius. Comparing the given equation with the general form of the equation of the circle. We get the values of g, f, and c as \[-2,-3\And 9\] respectively. We know that for a circle represented by the general form of the equation, the X and Y coordinates of the center are \[-g,-f\] respectively. Thus, for the given circle, by substituting the values of g and f, we get the coordinates of the center as \[\left( -(-2),-(-3) \right)\]. Simplifying this, we get center coordinates \[\left( 2,3 \right)\].
The radius of the circle is \[\sqrt{{{g}^{2}}+{{f}^{2}}-c}\], substituting the values of g, f, and c, we get radius as\[\sqrt{{{2}^{2}}+{{3}^{2}}-9}=2\].
The graph of the circle is as follows,

Note: We should remember for an equation of conic of form \[a{{x}^{2}}+b{{y}^{2}}+2gx+2fy+2hxy+c=0\] it must follow the following conditions to represent a circle. The first condition is \[a=b\]. The second condition is that \[h\] must be zero.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Class 11 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




