Question

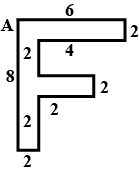
Find the centre of mass of the letter F which cut from a uniform metal sheet from point A.

$A.\quad \dfrac { 15 }{ 7 } ,\quad \dfrac { 33 }{ 7 }$
$B.\quad \dfrac { 15 }{ 7 } ,\quad \dfrac { 23 }{ 7 }$
$C.\quad \dfrac { 22 }{ 7 } ,\quad \dfrac { 33 }{ 7 }$
$D.\quad \dfrac { 33 }{ 7 } ,\quad \dfrac { 22 }{ 7 }$

Answer 1

Hint: Divide the letter F into 3 sections. Calculate their mass respectively. Note down coordinates of center of mass. And finally using the formula for Center of mass calculate position of center of mass.

Formula used:
$X_{ CM }=\quad \dfrac { \sum { { { m }_{ i }{ x }_{ i } } } }{ \sum { { m }_{ i } } }$
$Y_{ CM }=\quad \dfrac { \sum { { { m }_{ i }{ y }_{ i } } } }{ \sum { { m }_{ i } } }$

Complete step-by-step answer:
Figure given in the question can be simplified as:

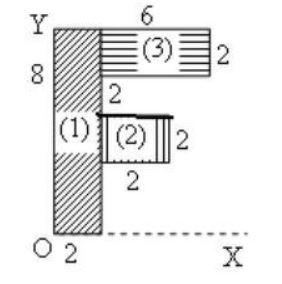
Let mass(m) per unit area(A)of the sheet be $\sigma$

$\sigma =\dfrac { m }{ A }$ …(1)

From the figure it is clear that the metal sheet is divided into 3 sections namely 1,2 and 3.

Using equation.(1), mass of each part can be calculated.

Mass of part 1, ${ m }_{ 1 }$= $\left( 8\times 2 \right) \sigma$= 16$\sigma$
Similarly, Mass of part 2, ${ m }_{ 2 }$= $\left( 2\times 2 \right) \sigma$= 4$\sigma$
Mass of part 3, ${ m }_{ 3 }$= $\left( 4\times 2 \right) \sigma$= 8$\sigma$

The coordinates of the center of mass of part1 are (1,4), that of part2 are (3,3) and that of part3 are (4,7).
Now, we have to calculate the center of mass of the letter F in X and Y- axes.
Using formula for center of mass in X-axis,

$X_{ CM }=\quad \dfrac { \sum { { { m }_{ i }{ x }_{ i } } } }{ \sum { { m }_{ i } } }$
$ { X }_{ CM }=\quad \dfrac { { m }_{ 1 }{ x }_{ 1 }+{ m }_{ 2 }{ x }_{ 2 }+{ m }_{ 3 }{ x }_{ 3 } }{ { m }_{ 1 }+{ m }_{ 2 }+{ m }_{ 3 } }$
Substituting the values in above equation we get,

$ { X }_{ CM }=\quad \dfrac { 16\sigma \times 1\quad +\quad 4\sigma \times 3\quad +\quad 8\sigma \times 4 }{ 16\sigma \quad +\quad 4\sigma \quad +\quad 8\sigma }$
$ \therefore \quad { X }_{ CM }=\quad \dfrac { 60 }{ 28 }$
$ \therefore \quad { X }_{ CM }=\quad \dfrac { 15 }{ 7 }$ …(1)

Similarly for Y-axis, using formula for center of mass,

$Y_{ CM }=\quad \dfrac { \sum { { { m }_{ i }{ y }_{ i } } } }{ \sum { { m }_{ i } } }$
$ { Y }_{ CM }=\quad \dfrac { { m }_{ 1 }{ y }_{ 1 }+{ m }_{ 2 }{ y }_{ 2 }+{ m }_{ 3 }{ y }_{ 3 } }{ { m }_{ 1 }+{ m }_{ 2 }+{ m }_{ 3 } }$

Substituting values in above equation we get,

$Y_{ CM }=\quad \dfrac { 16\sigma \times 4\quad +\quad 4\sigma \times 3\quad +\quad 8\sigma \times 7 }{ 16\sigma \quad +\quad 4\sigma \quad +\quad 8\sigma }$
$ \therefore \quad { Y }_{ CM }=\quad \dfrac { 132 }{ 28 }$
$ \therefore \quad { Y }_{ CM }=\quad \dfrac { 33 }{ 7 }$ …(2)

So, the correct answer is “Option A”.

Note:
Draw a simplified version of the figure so that calculation becomes easier. The simplified figure helps to find the length and co-ordinates easily. Take care while finding the coordinates of the center of mass of each part. A small error in the coordinates can change the answer completely.