Question

Find the coordinates of points of trisection of the line segment joining the points P (-3, 4) and Q (4, 5).

Answer 1

Hint: To solve this problem we need to have knowledge on trisection concept, section formula and basic calculation. Generally trisection means dividing the line segment in the ratio 1:2 or 2:1 internally.

Complete step-by-step answer:
Here we have to find the coordinates of point of trisection of a line segment that joining the given two points P and Q
We know that trisection divides the line segment in the ratio 1:2 or 2:1 internally.
Let the line segment be PQ.
Let A (x, y) divides the line segment PQ in the ratio 1:2.

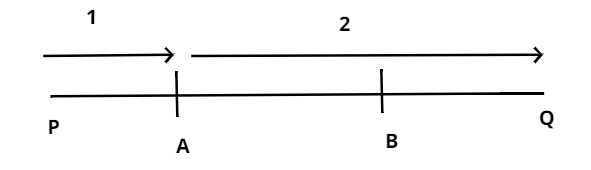
As we know that the section formula is
       $x = \dfrac{{m{x_2} + n{x_1}}}{{m + n}}$ ,$y = \dfrac{{m{y_2} + n{y_1}}}{{m + n}}$
Now by using the section formula let us find the A (x, y) coordinates, where the ratio m: n=1:2 and point are P (-3, 4) and Q (4, 5).
$x = \dfrac{{1 \times 4 + 2 \times - 3}}{{1 + 2}} = \dfrac{{ - 2}}{3}\left( {{x_1} = - 3,{x_2} = 4} \right)$
 $y = \dfrac{{1 \times 5 + 2 \times 4}}{{1 + 2}} = \dfrac{{13}}{3}\left( {{y_1} = 4,{y_2} = 5} \right)$
So the coordinates of A is $\left( {\dfrac{{ - 2}}{3},\dfrac{{13}}{3}} \right)$.
Similarly, let us find the coordinates of B (x, y) which divides the lines segment PQ in the ratio of 2:1

Now again by using the section formula let us find the B (x, y) coordinates, where the ratio m: n= 2: 1and point are P (-3, 4) and Q (4, 5).
              $x = \dfrac{{2 \times 4 + 1 \times - 3}}{{2 + 1}} = \dfrac{5}{3}\left( {{x_1} = - 3,{x_2} = 4} \right)$
              ${y_2} = \dfrac{{2 \times 5 + 1 \times 4}}{{2 + 1}} = \dfrac{{14}}{3}\left( {{y_1} = 4,{y_2} = 5} \right)$
So the coordinates of B is $\left( {\dfrac{5}{3},\dfrac{{14}}{3}} \right)$.
Hence the point of trisection are $\left( {\dfrac{5}{3},\dfrac{{14}}{3}} \right)$ and $\left( {\dfrac{{ - 2}}{3},\dfrac{{13}}{3}} \right)$

Note: Generally we get confused with trisection and section formula. Section formula locates the points on dividing the line segment in desired ratio, which means generally it helps us to find the coordinate points. And trisection means dividing the line segment into three equal parts or dividing the line segment in the ratio 1:2 or 2:1 internally.