
How do I find the directrix of a hyperbola?
Answer
470.1k+ views
Hint: Here we need to draw the figure of general hyperbola which is
Complete step by step solution:
Here we need to find the equation of the directrix of the hyperbola. For this, we must know what the equation and the representation of hyperbola are. So let us consider hyperbola as represented below:
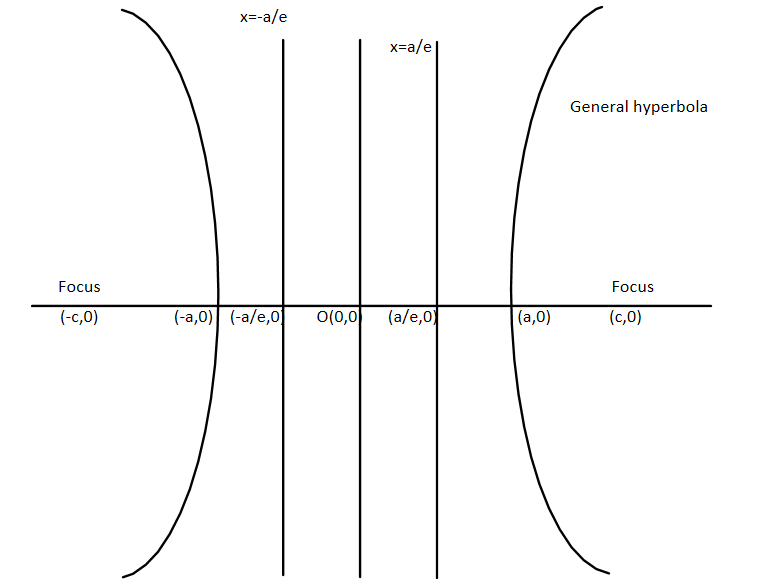
Here we can see that this is the general hyperbola and its general equation is given by:
Here the axis on which the vertex is there is called the transverse axis and another is called the conjugate axis.
Now we can see that focus is given by
The directrix is the line which is parallel to y axis and is given by
This can be made clear with an example:
Let us have the hyperbola where we have
So we can compare this above equation with
Hence we can now calculate the value of
Now we know that directrix of hyperbola is given by
Substituting the values we get:
So
Note:
Here the student must know every formula of the general hyperbola because this will be helpful to calculate the results faster and also when we shift the hyperbola centre from origin to any other point.
Complete step by step solution:
Here we need to find the equation of the directrix of the hyperbola. For this, we must know what the equation and the representation of hyperbola are. So let us consider hyperbola as represented below:

Here we can see that this is the general hyperbola and its general equation is given by:
Here the axis on which the vertex is there is called the transverse axis and another is called the conjugate axis.
Now we can see that focus is given by
The directrix is the line which is parallel to y axis and is given by
This can be made clear with an example:
Let us have the hyperbola where we have
So we can compare this above equation with
Hence we can now calculate the value of
Now we know that directrix of hyperbola is given by
Substituting the values we get:
So
Note:
Here the student must know every formula of the general hyperbola because this will be helpful to calculate the results faster and also when we shift the hyperbola centre from origin to any other point.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Which one of the following is a true fish A Jellyfish class 12 biology CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Write the difference between solid liquid and gas class 12 chemistry CBSE




