Question

How do you find the distance between two parallel lines in 3-dimensional space?

Answer 1

Hint: In the above question, we are given two parallel lines in a 3-dimensional space. We have to find the distance between those two given lines. Recall the formula of cross product of two vectors. The cross product of two vectors is itself a vector and is given by the formula \[\overrightarrow a \times \overrightarrow b = \left| a \right|\left| b \right|\sin \theta \widehat n\], where \[\widehat n\] is the unit vector in the perpendicular direction of both vectors. This formula will be useful in finding the required distance, let see how.

Complete step by step answer:
Given that, two parallel lines that lie in a 3-dimensional space. Let the two parallel lines be \[{l_1}\] and \[{l_2}\]. Let the equations of the two parallel lines be,
\[{l_1} \Rightarrow \overrightarrow r = \overrightarrow {{a_1}} + \lambda \overrightarrow b \]
And
\[{l_2} \Rightarrow \overrightarrow r = \overrightarrow {{a_2}} + \mu \overrightarrow b \]
Where \[\overrightarrow {{a_1}} \] and \[\overrightarrow {{a_2}} \] are points on \[{l_1}\] and \[{l_2}\] and \[\overrightarrow b \] is the line parallel to both \[{l_1}\] and \[{l_2}\] .

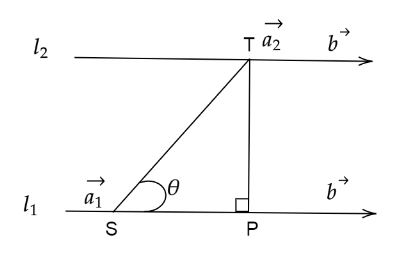
A diagram of both the lines is shown above where the distance between \[{l_1}\] and \[{l_2}\] is PT. Consider the vectors \[\overrightarrow {ST} \] and \[\overrightarrow b \] , their cross product can be written using the formula,
\[ \Rightarrow \overrightarrow a \times \overrightarrow b = \left| a \right|\left| b \right|\sin \theta \,\widehat n\]
As,
\[ \Rightarrow \overrightarrow b \times \overrightarrow {ST} = \left| {\overrightarrow b } \right|\left| {\overrightarrow {ST} } \right|\sin \theta \cdot \widehat n\] ...(1)
Also the distance ST can be written as,
\[\overrightarrow {ST} = \overrightarrow {{a_2}} - \overrightarrow {{a_1}} \] ...(2)

Now from the diagram, we have
\[ \Rightarrow \sin \theta = \left| {\dfrac{{PT}}{{ST}}} \right|\]
That gives,
\[ \Rightarrow \left| {ST} \right|\sin \theta = \left| {PT} \right|\]
Multiplying both sides by \[\left| {\overrightarrow b } \right| \cdot \widehat n\] , we get
\[ \Rightarrow \left| {\overrightarrow b } \right|\left| {ST} \right|\sin \theta \cdot \widehat n = \left| {\overrightarrow b } \right| \cdot \left| {PT} \right| \cdot \widehat n\]
Now, using the equation ...(1) we can write the above equation as
\[ \Rightarrow \overrightarrow b \times \overrightarrow {ST} = \left| {\overrightarrow b } \right|\left| {PT} \right| \cdot \widehat n\]
Taking modulus of both sides,
\[ \Rightarrow \left| {\overrightarrow b \times \overrightarrow {ST} } \right| = \left| {\overrightarrow b } \right|\left| {PT} \right| \cdot \left| {\widehat n} \right|\]

Since \[\left| {\widehat n} \right| = 1\] that gives,
\[ \Rightarrow \left| {\overrightarrow b \times \overrightarrow {ST} } \right| = \left| {\overrightarrow b } \right|\left| {PT} \right|\]
Again, putting \[\overrightarrow {ST} = \overrightarrow {{a_2}} - \overrightarrow {{a_1}} \] we get
\[ \Rightarrow \left| {\overrightarrow b \times \left( {\overrightarrow {{a_2}} - \overrightarrow {{a_1}} } \right)} \right| = \left| {\overrightarrow b } \right|\left| {PT} \right|\]
\[ \therefore \left| {PT} \right| = \dfrac{{\left| {\overrightarrow b \times \left( {\overrightarrow {{a_2}} - \overrightarrow {{a_1}} } \right)} \right|}}{{\left| {\overrightarrow b } \right|}}\]
That is the required distance between the two parallel lines \[{l_1}\] and \[{l_2}\].

Therefore, the distance between two parallel lines in a 3-dimensional space is given by \[\dfrac{{\left| {\overrightarrow b \times \left( {\overrightarrow {{a_2}} - \overrightarrow {{a_1}} } \right)} \right|}}{{\left| {\overrightarrow b } \right|}}\].

Note: In three-dimensional geometry, skew lines are two lines that do not intersect and also are not parallel. As a result they do not lie in the same plane. A simple example of a pair of skew lines is the pair of lines through opposite edges of a regular tetrahedron. While intersecting lines and parallel lines lie in the same plane i.e. are coplanar.