
How do you find the domain and range for
Answer
431.1k+ views
Hint: We can think of the cot function as the inverse tangent function or we can think of it as the fraction of sine and cosine. Keeping those in mind we can find the range and domain of the cot function. We need to be aware of its graph as well. By seeing the graph it can easily be figured out what the range and domain are for the function of cotangent.
Complete step-by-step solution:
We have
Now, whenever the tangent function will be 0, the function of cotangent will not be defined. And we know that at
Now, we find the range of the cot function. For this we say that tangent takes all values of the real line. So, the range of cot will also be all the real numbers or
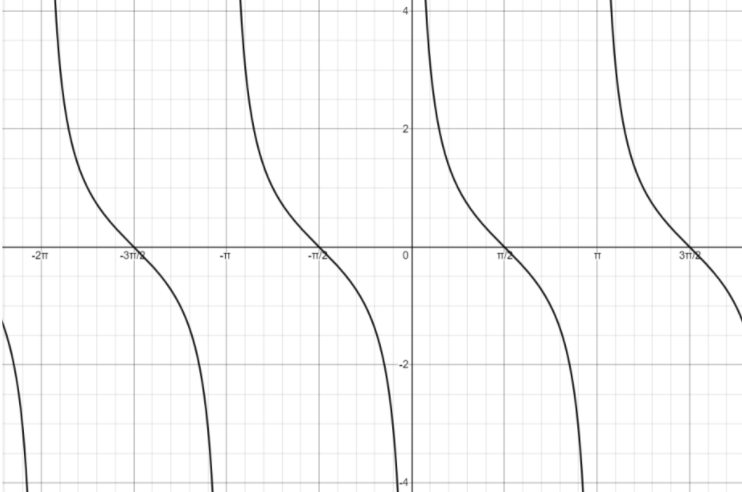
Hence, the domain and range has been found out.
Note: You can think of the domain as all the possible
Complete step-by-step solution:
We have
Now, whenever the tangent function will be 0, the function of cotangent will not be defined. And we know that at
Now, we find the range of the cot function. For this we say that tangent takes all values of the real line. So, the range of cot will also be all the real numbers or

Hence, the domain and range has been found out.
Note: You can think of the domain as all the possible
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Write the differences between monocot plants and dicot class 11 biology CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

In northern hemisphere 21st March is called as A Vernal class 11 social science CBSE




