Question

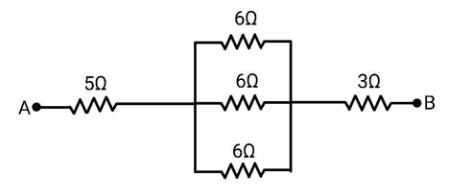
Find the effective resistance between A and B

Answer 1

Hint: Here, we are supposed to find the effective resistance between the point A and B, meaning that we are supposed to find a value of single resistance which will offer equal resistance as offered by the combination of these five resistors. A circuit might contain a number of resistors but in most of the cases, the circuit can be reduced and the number of resistors can be decreased by equivalent resistors. The reduction can be obtained by finding series and parallel combinations of resistors.

Complete step by step answer:
Whenever you want to find if the resistors are connected in series or in parallel, always go for the end points of the resistors. Consider two resistors, if one end of each resistor is connected at the same point, you say that the resistors are connected in series and if both the ends of the resistors meet at the same point, then you say that the resistors are connected in parallel. Now, observe the figure given in the question, you can see that the ends of all the $6\Omega $ resistors meet at the same point, that is, the left ends of all the resistors meet at the left junction and the right ends of all the resistors meet at the right junction. So, all the $6\Omega $ resistors are connected in parallel.

When a parallel combination of $n$ resistors is given and you are asked to find the equivalent resistance, the equivalent resistor ${R_{eq}}$ is given as $\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} + ...$ all the way up to ${R_n}$. As all the $6\Omega $ resistors are in parallel, the equivalent resistance of these $6\Omega $ resistances will be,
${R_{e{q_1}}} = \dfrac{1}{{\dfrac{1}{6} + \dfrac{1}{6} + \dfrac{1}{6}}}\\
\Rightarrow{R_{e{q_1}}} = \dfrac{1}{{\dfrac{3}{6}}} \\
\Rightarrow{R_{e{q_1}}}= 2\Omega $
Now, you can observe that the $5\Omega $ resistor, the $3\Omega $ resistor and the $2\Omega $ equivalent resistor are in series. Take any two resistance, you can see that they have only one point in common. When the resistances are in series, the equivalent resistance is simply the sum of the resistances connected in series. Therefore, the net effective resistance in between point A and B is ${R_{eff}} = 5 + 2 + 3 = 10\Omega $.

Hence, the effective resistance between point A and B is $10\Omega $.

Note: Make sure that you keep in mind the method of reducing the circuit having resistances to its lowest form, it may be a case where the resistances are connected in series, or say in parallel and it may be the case where the resistances are connected as a combination of series and parallel. Keep in mind how the equivalent/effective value of resistance is obtained in case of series and parallel. In series, the effective resistance is simply the sum of resistances and in parallel the reciprocal of the effective resistance is equal to the sum of the reciprocals of each resistance.