Question

Find the equation of a sphere which passes through the circle ${{x}^{2}}+{{y}^{2}}=4$, z = 0 and is cut by the plane $x+2y+2z=0$ in a circle of radius 3.

Answer 1

Hint:First write the general equation of a sphere which is ${{x}^{2}}+{{y}^{2}}+2gx+2fy+2hz+c=0$ then put z = 0 in this equation. We can find the centre and radius of a sphere from the equation of a sphere as the centre of a sphere is (-g, -f, -h) and radius of a sphere is $\sqrt{{{g}^{2}}+{{f}^{2}}+{{h}^{2}}-c}$. Now as the sphere is passing through a circle so we can compare the equation of the sphere with the circle and find the centre and radius from it. Then drop a perpendicular from the centre of the sphere to the plane and then apply Pythagoras theorem and get all the remaining unknowns.

Complete step-by-step answer:
The general equation of a sphere is:
${{x}^{2}}+{{y}^{2}}+2gx+2fy+2hz+c=0$
It is given that the sphere passes through z = 0. Plugging z = 0 in the above equation we get,
${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$
We know that if a sphere equation is given then we can find the centre and radius of a sphere as follows:
Centre of a sphere is (-g, -f, -h).
Radius of a sphere is $\sqrt{{{g}^{2}}+{{f}^{2}}+{{h}^{2}}-c}$.
Now, it is also given that the sphere passes through the equation of circle ${{x}^{2}}+{{y}^{2}}=4$ so comparing equation of a circle with the sphere we get,
${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$
${{x}^{2}}+{{y}^{2}}-4=0$
On comparing the above two equations we get, g = 0, f = 0, c = -4.
Substituting the value of g, f and c in the formula of centre and radius of a sphere we get,
The centre of the sphere is (0, 0, -h) and the radius of the sphere is $\sqrt{{{h}^{2}}+4}$.
Now in the figure below, a plane $x+2y+2z=0$ cuts the sphere in a circle of radius equal 3.

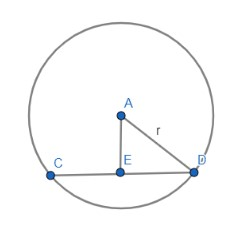
As you can see from the figure that the sphere is centred at A and CD is the diameter of a circle cut by the plane. AD is the radius of the sphere and AD is the perpendicular drawn from point A to the plane.
Applying Pythagoras theorem in the $\Delta AED$ we get,
AD2 = AE2 + ED2
AE is the perpendicular drawn from a point A to the plane. The length of the perpendicular drawn from a point A (0, 0, h) to the plane $x+2y+2z=0$ is equal to $\dfrac{2h}{3}$.
ED is the radius of the circle cut by the plane on the sphere and is equal to 3.
AD = $\sqrt{{{h}^{2}}+4}$
Substituting these values in Pythagoras theorem we get,
$\begin{align}
  & {{h}^{2}}+4=\dfrac{4{{h}^{2}}}{9}+9 \\
 & \Rightarrow 9{{h}^{2}}+36=4{{h}^{2}}+81 \\
 & \Rightarrow 5{{h}^{2}}=45 \\
 & \Rightarrow {{h}^{2}}=9 \\
 & \Rightarrow h=\pm 3 \\
\end{align}$
When h = 3, the equation of sphere is ${{x}^{2}}+{{y}^{2}}+6z-4=0$.
And when h = -3, the equation of a sphere is ${{x}^{2}}+{{y}^{2}}-6z-4=0$.

Note: As in the above solution, we have written the length of the perpendicular from a point A to the plane $x+2y+2z=0$. We are going to show how this length of perpendicular has come.
We know the formula for the perpendicular distance from a point $P\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)$ to the plane $ax+by+cz=0$ is:
$\dfrac{\left| a{{x}_{1}}+b{{y}_{1}}+c{{z}_{1}} \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}$
Now, we are evaluating the perpendicular distance from a point A (0, 0, -h) to the plane $x+2y+2z=0$ using the above formula where ${{x}_{1}}=0,{{y}_{1}}=0,z=-h$ and $a=1,b=2,c=2$ we get,
$\begin{align}
  & \dfrac{\left| 0+0-2h \right|}{\sqrt{1+{{2}^{2}}+{{2}^{2}}}} \\
 & =\dfrac{2h}{3} \\
\end{align}$.