Question

Find the equation of the circle if the circle passes through the points (0, 0), (8, 0) and (0, 9).

Answer 1

Hint: First we will find the center and radius of the circle using distance formula and then we will find the equation of the circle from obtained data
Distance Formula, \[d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\]

Complete step by step answer:
Given that we have to find the equation of a circle passing through points (0, 0), (8, 0) and (0, 9) respectively.

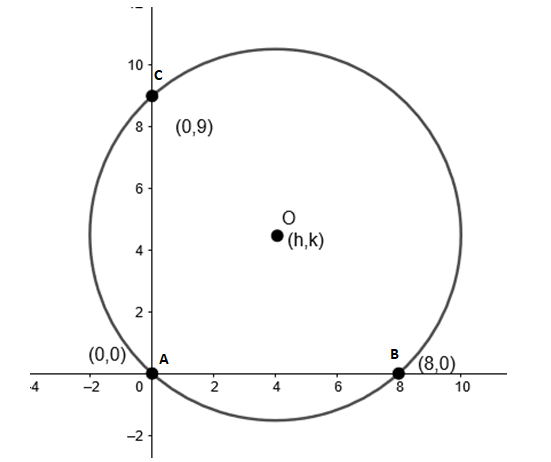
Let us assume that the center of the circle is at O.
Coordinates of O are (h, k).
Now, we know that the radius of the circle is of equal length. (Property of Circle)
We get, AO = BO = CO
AO, BO and CO are the radii of the circle, thus they are of equal length.
Also, from distance formula between two points, i.e. \[\left( {{x}_{1}},{{y}_{1}} \right)\] and \[\left( {{x}_{2}},{{y}_{2}} \right)\]
\[d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\]
where d is the distance between two points.
Applying this between AO and BO as both are the radii of the circle,
\[AO=BO\]
\[\Rightarrow \sqrt{{{\left( h-0 \right)}^{2}}+{{\left( k-0 \right)}^{2}}}=\sqrt{{{\left( h-8 \right)}^{2}}+{{\left( k-0 \right)}^{2}}}\]
\[\Rightarrow \sqrt{{{h}^{2}}+{{0}^{2}}-2\left( 0 \right)\left( h \right)+{{k}^{2}}+{{0}^{2}}-2\left( 0 \right)\left( k \right)}=\sqrt{{{h}^{2}}+{{8}^{2}}-2\left( 8 \right)\left( h \right)+{{k}^{2}}+{{0}^{2}}-2\left( 0 \right)\left( k \right)}\]
\[\Rightarrow \sqrt{{{h}^{2}}+{{k}^{2}}}=\sqrt{{{h}^{2}}+{{k}^{2}}+64-16h}\]
Squaring both sides, we get
\[\Rightarrow {{h}^{2}}+{{k}^{2}}={{h}^{2}}+{{k}^{2}}+64-16h\]
Canceling the similar terms, from both sides, we get,
\[\Rightarrow 64-16h=0\]
\[\Rightarrow 16h=64\]
\[\Rightarrow h=\dfrac{64}{16}\]
\[\Rightarrow h=4\]
Similarly, from AO = BO, we will again perform the same calculation for AO = CO.
We know that,
\[d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\]
Putting the values of AO and CO, we get
\[\Rightarrow \sqrt{{{\left( h-0 \right)}^{2}}+{{\left( k-0 \right)}^{2}}}=\sqrt{{{\left( h-0 \right)}^{2}}+{{\left( k-9 \right)}^{2}}}\]
\[\Rightarrow \sqrt{{{h}^{2}}+{{0}^{2}}-2\left( h \right)\left( 0 \right)+{{k}^{2}}+{{0}^{2}}-2\left( 0 \right)\left( k \right)}=\sqrt{{{h}^{2}}+{{0}^{2}}-2\left( h \right)\left( 0 \right)+{{k}^{2}}+81-2\left( 9 \right)\left( k \right)}\]
\[\Rightarrow \sqrt{{{h}^{2}}+{{k}^{2}}}=\sqrt{{{h}^{2}}+{{k}^{2}}+81-18k}\]
Squaring both sides, we get
\[\Rightarrow {{h}^{2}}+{{k}^{2}}={{h}^{2}}+{{k}^{2}}+81-18k\]
Canceling equal terms from both sides, we get
\[\Rightarrow 81-18k=0\]
\[\Rightarrow 18k=81\]
\[\Rightarrow k=\dfrac{81}{18}\]
\[k=4.5\]
Now, we are ready with our center coordinates.
\[h=4,\text{ }k=4.5\]
\[\left( h,k \right)=\left( 4,4.5 \right)\]
We know that radius of the circle \[=\sqrt{{{h}^{2}}+{{k}^{2}}}\]
Putting the value of h and k, we get
\[=\sqrt{{{h}^{2}}+{{k}^{2}}}\]
\[=\sqrt{{{\left( 4 \right)}^{2}}+{{\left( 4.5 \right)}^{2}}}\]
\[=\sqrt{16+20.25}\]
\[=\sqrt{36.25}\]
\[=6.042\]
Now, we are ready with all the required values to form an equation of the circle.
We know that the general equation of the circle is \[{{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{\left( r \right)}^{2}}\]
Substituting values of (h, k) and r in the general equation of the circle, we get
\[\Rightarrow {{\left( x-4 \right)}^{2}}+{{\left( y-4.5 \right)}^{2}}={{\left( 6.042 \right)}^{2}}\]
\[\Rightarrow {{x}^{2}}+16-8x+{{y}^{2}}+20.25-9k=36.25\]
\[\Rightarrow {{x}^{2}}+{{y}^{2}}-8x-9y=0\]
Thus, the required equation of the circle is \[{{x}^{2}}+{{y}^{2}}-8x-9y=0\]

Note: Alternate Method:
You can solve this question by using the following steps.
1. Substitute the values of the given point in the general equation of the circle.
2. Find the values of the unknowns i.e. (h, k) and r.
3. Form the required equation of the circle.