Question

Find the equation of the parabola if the focus is at $\left( 0,0 \right)$ and the vertex is at the intersection of the lines $x+y=1$ and $x-y=3$?

Answer 1

Hint: We start solving the problem by finding the vertex of the parabola using the intersection of lines. We then find the equation of the axis of the parabola and the point of intersection of the axis and directrix of parabola using the fact that the directrix of the parabola is perpendicular to its axis. We then slope the directrix using the fact that the product of slopes of perpendicular lines is ‘–1’, using this we find the equation of the directrix. We then assume the point on the parabola and use the fact that this point is at an equal distance from focus and directrix. We then make the necessary calculations to get the required equation of parabola.

Complete step by step answer:
According to the problem, we need to find the equation of the parabola such that the focus is at $\left( 0,0 \right)$ and the vertex is at the intersection of the lines $x+y=1$ and $x-y=3$.
Let us first find the vertex of the parabola.
So, let us substitute $x=3+y$ in the line $x+y=1$.
$\Rightarrow 3+y+y=1$.
$\Rightarrow 2y=-2$.
$\Rightarrow y=-1$. Let us substitute this value from $x+y=1$.
So, we get $x-1=1\Leftrightarrow x=2$.
So, the vertex of the parabola is $\left( 2,-1 \right)$.
Now, let us find the equation of the parabola with the focus $\left( 0,0 \right)$ and vertex $\left( 2,-1 \right)$.
Let us find the equation of the axis of the parabola.
We know that the equation of the line passing through the points $\left( {{x}_{1}},{{y}_{1}} \right)$, $\left( {{x}_{2}},{{y}_{2}} \right)$ is $y-{{y}_{1}}=\left( \dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} \right)\times \left( x-{{x}_{1}} \right)$.
So, the equation of the axis is $y-0=\left( \dfrac{-1-0}{2-0} \right)\times \left( x-0 \right)$.
$\Rightarrow y=\dfrac{-1}{2}\times x$.
$\Rightarrow y=\dfrac{-x}{2}$ ---(1).
Comparing this with the equation of the line $y=mx+c$, we get the slope of the axis as $\dfrac{-1}{2}$.
We know that the directrix of the parabola is perpendicular to its axis. We also know that the slopes of the perpendicular lines is –1.
Let us assume the slope of the directrix is ${{m}_{d}}$. So, we get ${{m}_{d}}\times \dfrac{-1}{2}=-1$.
$\Rightarrow {{m}_{d}}=2$.
We know that the vertex is the midpoint of focus and point of intersection of the directrix and axis of parabola.
So, let us assume the point of intersection of the directrix and axis of the parabola is $\left( a,b \right)$.
So, we get $\left( 2,-1 \right)=\left( \dfrac{0+a}{2},\dfrac{0+b}{2} \right)$.
$\Rightarrow \dfrac{0+a}{2}=2$ and $\dfrac{0+b}{2}=-1$.
$\Rightarrow a=4$ and $b=-2$.
So, the point of intersection of the directrix and axis of the parabola is $\left( 4,-2 \right)$.
Now, we need to find the equation of the directrix which is passing through the point $\left( 4,-2 \right)$ and having slope ‘2’.
We know that the equation of the line passing through the points $\left( {{x}_{1}},{{y}_{1}} \right)$ and having slope ‘m’ is $y-{{y}_{1}}=m\times \left( x-{{x}_{1}} \right)$.
So, the equation of the directrix is $y-\left( -2 \right)=2\left( x-4 \right)$.
$\Rightarrow y+2=2x-8$.
$\Rightarrow 2x-y-10=0$.

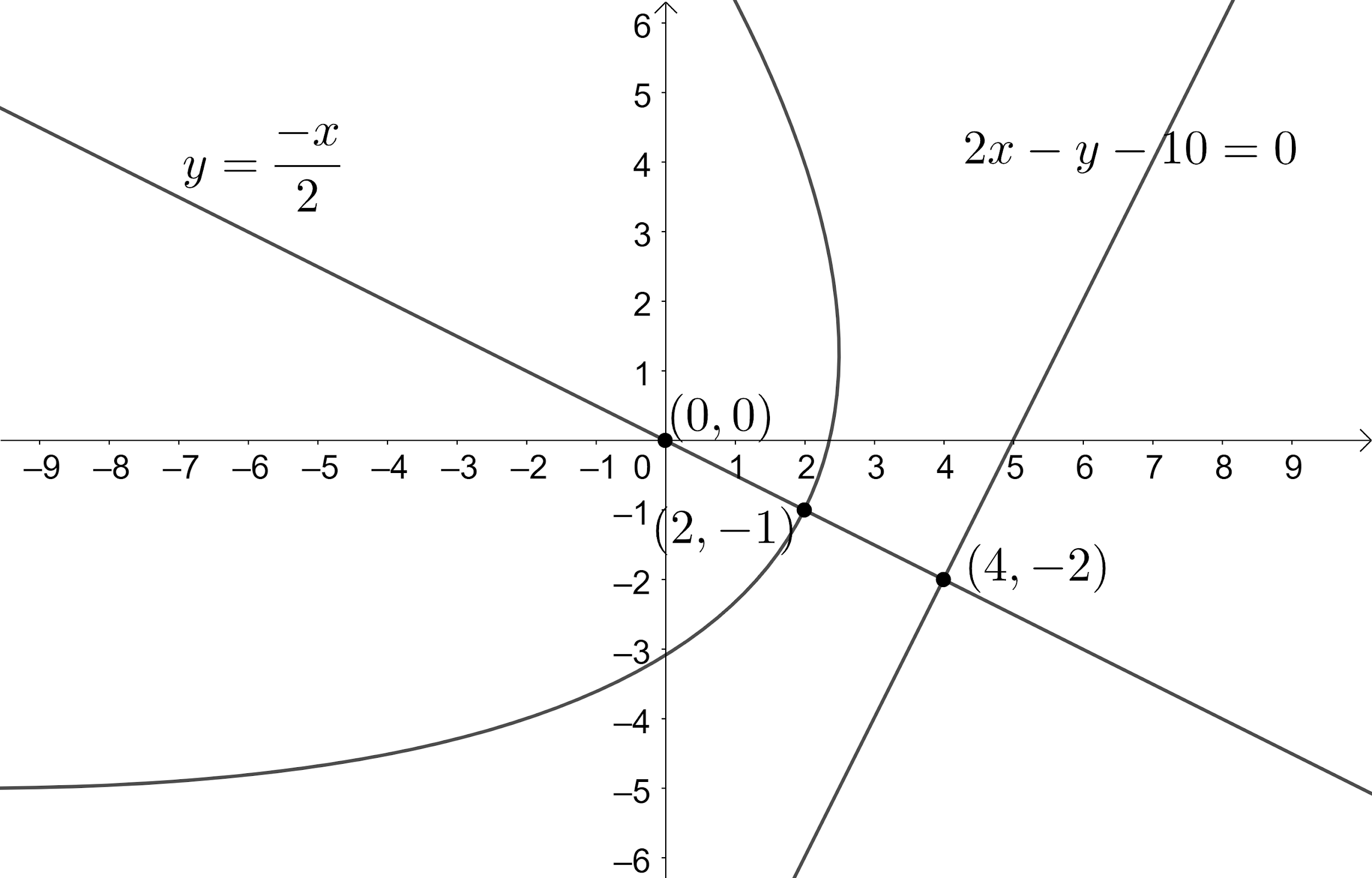
Now, let us assume the point $\left( l,m \right)$ be the point on the parabola. We know that this point is at an equal distance from the directrix and focus.
We know that the distance between two points $\left( {{x}_{1}},{{y}_{1}} \right)$, $\left( {{x}_{2}},{{y}_{2}} \right)$ is $\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$ and the perpendicular distance from the point $\left( {{x}_{1}},{{y}_{1}} \right)$ to the line $ax+by+c=0$ is $\dfrac{\left| a{{x}_{1}}+b{{y}_{1}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$.
So, we get $\sqrt{{{\left( l-0 \right)}^{2}}+{{\left( m-0 \right)}^{2}}}=\dfrac{\left| 2l-m-10 \right|}{\sqrt{{{2}^{2}}+{{\left( -1 \right)}^{2}}}}$.
$\Rightarrow \sqrt{{{l}^{2}}+{{m}^{2}}}=\dfrac{\left| 2l-m-10 \right|}{\sqrt{4+1}}$.
$\Rightarrow \sqrt{{{l}^{2}}+{{m}^{2}}}=\dfrac{\left| 2l-m-10 \right|}{\sqrt{5}}$.
Let us square on both sides.
$\Rightarrow {{\left( \sqrt{{{l}^{2}}+{{m}^{2}}} \right)}^{2}}=\dfrac{{{\left| 2l-m-10 \right|}^{2}}}{{{\left( \sqrt{5} \right)}^{2}}}$.
$\Rightarrow {{l}^{2}}+{{m}^{2}}=\dfrac{4{{l}^{2}}+{{m}^{2}}+100-4lm+20m-40l}{5}$.
$\Rightarrow 5{{l}^{2}}+5{{m}^{2}}=4{{l}^{2}}+{{m}^{2}}+100-4lm+20m-40l$.
$\Rightarrow {{l}^{2}}+4{{m}^{2}}+4lm+40l-20m-100=0$.
Let us replace ‘l’, ‘m’ with ‘x’, ‘y’ to get the equation of parabola.
$\Rightarrow {{x}^{2}}+4{{y}^{2}}+4xy+40x-20y-100=0$.

So, we have found the required equation of the parabola as ${{x}^{2}}+4{{y}^{2}}+4xy+40x-20y-100=0$.

Note: We should not use ${{\left( y-p \right)}^{2}}=4a\left( x-q \right)$, where $\left( p,q \right)$ is vertex and $a$ is the distance between focus and vertex as this equation is valid only if the axis is parallel to x-axis. Here we replaced ‘l’, ‘m’ with ‘x’, ‘y’ in order to get the locus of all points that were present on the parabola. We should first see what is the axis of the parabola to proceed through the problem as it tells us whether we can use the standard forms of parabola or not. We can see that this problem contains a good amount of calculations, so we should make mistakes while solving this problem.