Find the equation of the tangent line to the circle ${{(x+2)}^{2}}+{{(y-3)}^{2}}=25$ at the point $A$ $(-5,7)$.
Answer
Verified362.4k+ views
Hint: Assume a line with a variable slope, passing through the point $(-5,7)$ and then make the perpendicular distance of the centre of the circle equal to the radius of the circle, to get the slope, and eventually the tangent.
First, let’s analyse the equation of the circle given to us :
${{(x+2)}^{2}}+{{(y-3)}^{2}}=25$, by comparing it to the general equation of a circle which is ${{(x+g)}^{2}}+{{(y+f)}^{2}}={{r}^{2}}$, where the centre of the circle is $(-g,-f)$ and the radius of the circle is $r$.
Comparing the equation given to us with the general equation, we get :
$g=2,f=-3,r=\sqrt{25}=5$
Thus, the centre of this circle is = $(-g,-f)=(-2,3)$ and its radius $=5$
Now, to find the tangent passing through the point $A$, let’s assume a line whose equation can be written as :
$\begin{align}
& \dfrac{y-7}{x+5}=m \\
& \Rightarrow y-7=mx+5m \\
& \Rightarrow y=mx+5m+7 \\
& \Rightarrow mx-y+(5m+7)=0 \\
\end{align}$
since it’s mandatory for the tangent to pass through point $A$, and this is how the equation of a line passing through a given point is written as.
Let’s call this equation of tangent in terms of $m$ as (1).
Now, we know that the tangent is perpendicular to the line joining the centre of the circle to the point where the tangent touches the circle. This means that the tangent is perpendicular to the line representing the radius of the circle at the point $A$.
This implies that the perpendicular distance of the centre of the circle from the tangent will be equal to the circle’s radius.
$\Rightarrow d=r$ where $d$ is the perpendicular distance of the centre from (1) and $r$ is the circle’s radius.
The formula to find the perpendicular distance of a point $(X,Y)$ from a line $Ax+By+C=0$ is :
$d=\dfrac{|AX+BY+C|}{\sqrt{{{A}^{2}}+{{B}^{2}}}}$
Here, the point we have to find the perpendicular distance for is the centre $(-g,-f)=(-2,3)$ , and the line we have to find it from is (1) or $mx-y+(5m+7)=0$
$\begin{align}
& \Rightarrow d=\dfrac{|AX+BY+C|}{\sqrt{{{A}^{2}}+{{B}^{2}}}} \\
& \Rightarrow d=\dfrac{|-2m-3+5m+7|}{\sqrt{{{m}^{2}}+1}} \\
\end{align}$
But, we know that for this question, $d=r=5$
$\begin{align}
& \Rightarrow r=\dfrac{|3m+4|}{\sqrt{{{m}^{2}}+1}} \\
& \Rightarrow 5=\dfrac{|3m+4|}{\sqrt{{{m}^{2}}+1}} \\
\end{align}$
Squaring both sides, we get :
$\begin{align}
& \Rightarrow 25=\dfrac{{{(3m+4)}^{2}}}{{{m}^{2}}+1} \\
& \Rightarrow 25({{m}^{2}}+1)=9{{m}^{2}}+16+24m \\
& \Rightarrow 25{{m}^{2}}+25=9{{m}^{2}}+16+24m \\
& \Rightarrow 16{{m}^{2}}-24m+9=0 \\
& \Rightarrow 16{{m}^{2}}-12m-12m+9=0 \\
& \Rightarrow 4m(4m-3)-3(4m-3)=0 \\
& \Rightarrow {{(4m-3)}^{2}}=0 \\
& \Rightarrow m=\dfrac{3}{4} \\
\end{align}$
Substituting the value of $m$ obtained in (1), we get the final equation of the tangent as :
$\begin{align}
& mx-y+(5m+7)=0 \\
& \Rightarrow \dfrac{3}{4}x-y+(5\times \dfrac{3}{4}+7)=0 \\
& \Rightarrow \dfrac{3}{4}x-y+\dfrac{43}{4}=0 \\
& \Rightarrow 3x-4y+43=0 \\
\end{align}$
Here’s a diagram to ease your understanding :
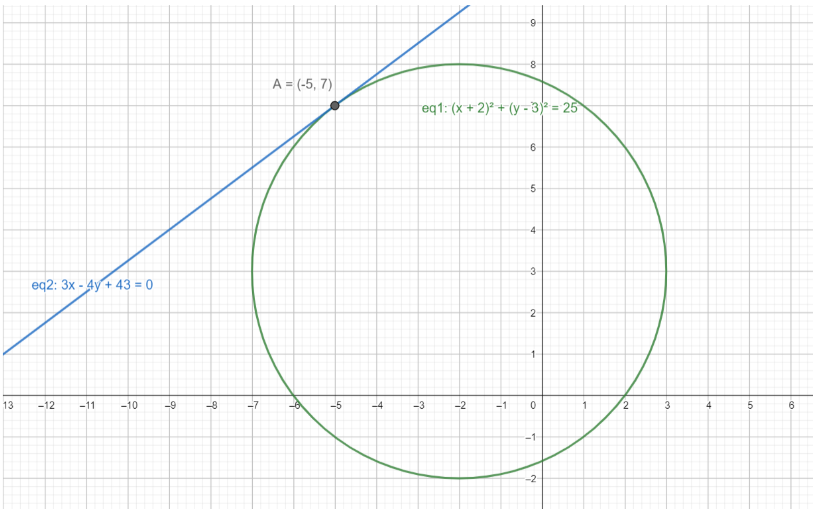
As you can see, eq2 is the tangent to the circle with eq1, and it is a tangent at the point $A=(-5,7)$.
Hence, our final equation of the tangent to ${{(x+2)}^{2}}+{{(y-3)}^{2}}=25$ at the point $A$ $(-5,7)$ is $3x-4y+43=0$.
So the answer to the required equation is $3x-4y+43=0$.
Note: Be careful while working with modulus. While squaring a modulus, we can simply square the expression that’s present inside the modulus, rather than considering both the positive and negative possibilities of the expression. This is because whatever the expression is, the square of a negative number and a positive number of the same magnitude, are always equal. Thus, we can simply square the expression inside the modulus, without having to worry about the sign.
First, let’s analyse the equation of the circle given to us :
${{(x+2)}^{2}}+{{(y-3)}^{2}}=25$, by comparing it to the general equation of a circle which is ${{(x+g)}^{2}}+{{(y+f)}^{2}}={{r}^{2}}$, where the centre of the circle is $(-g,-f)$ and the radius of the circle is $r$.
Comparing the equation given to us with the general equation, we get :
$g=2,f=-3,r=\sqrt{25}=5$
Thus, the centre of this circle is = $(-g,-f)=(-2,3)$ and its radius $=5$
Now, to find the tangent passing through the point $A$, let’s assume a line whose equation can be written as :
$\begin{align}
& \dfrac{y-7}{x+5}=m \\
& \Rightarrow y-7=mx+5m \\
& \Rightarrow y=mx+5m+7 \\
& \Rightarrow mx-y+(5m+7)=0 \\
\end{align}$
since it’s mandatory for the tangent to pass through point $A$, and this is how the equation of a line passing through a given point is written as.
Let’s call this equation of tangent in terms of $m$ as (1).
Now, we know that the tangent is perpendicular to the line joining the centre of the circle to the point where the tangent touches the circle. This means that the tangent is perpendicular to the line representing the radius of the circle at the point $A$.
This implies that the perpendicular distance of the centre of the circle from the tangent will be equal to the circle’s radius.
$\Rightarrow d=r$ where $d$ is the perpendicular distance of the centre from (1) and $r$ is the circle’s radius.
The formula to find the perpendicular distance of a point $(X,Y)$ from a line $Ax+By+C=0$ is :
$d=\dfrac{|AX+BY+C|}{\sqrt{{{A}^{2}}+{{B}^{2}}}}$
Here, the point we have to find the perpendicular distance for is the centre $(-g,-f)=(-2,3)$ , and the line we have to find it from is (1) or $mx-y+(5m+7)=0$
$\begin{align}
& \Rightarrow d=\dfrac{|AX+BY+C|}{\sqrt{{{A}^{2}}+{{B}^{2}}}} \\
& \Rightarrow d=\dfrac{|-2m-3+5m+7|}{\sqrt{{{m}^{2}}+1}} \\
\end{align}$
But, we know that for this question, $d=r=5$
$\begin{align}
& \Rightarrow r=\dfrac{|3m+4|}{\sqrt{{{m}^{2}}+1}} \\
& \Rightarrow 5=\dfrac{|3m+4|}{\sqrt{{{m}^{2}}+1}} \\
\end{align}$
Squaring both sides, we get :
$\begin{align}
& \Rightarrow 25=\dfrac{{{(3m+4)}^{2}}}{{{m}^{2}}+1} \\
& \Rightarrow 25({{m}^{2}}+1)=9{{m}^{2}}+16+24m \\
& \Rightarrow 25{{m}^{2}}+25=9{{m}^{2}}+16+24m \\
& \Rightarrow 16{{m}^{2}}-24m+9=0 \\
& \Rightarrow 16{{m}^{2}}-12m-12m+9=0 \\
& \Rightarrow 4m(4m-3)-3(4m-3)=0 \\
& \Rightarrow {{(4m-3)}^{2}}=0 \\
& \Rightarrow m=\dfrac{3}{4} \\
\end{align}$
Substituting the value of $m$ obtained in (1), we get the final equation of the tangent as :
$\begin{align}
& mx-y+(5m+7)=0 \\
& \Rightarrow \dfrac{3}{4}x-y+(5\times \dfrac{3}{4}+7)=0 \\
& \Rightarrow \dfrac{3}{4}x-y+\dfrac{43}{4}=0 \\
& \Rightarrow 3x-4y+43=0 \\
\end{align}$
Here’s a diagram to ease your understanding :
As you can see, eq2 is the tangent to the circle with eq1, and it is a tangent at the point $A=(-5,7)$.
Hence, our final equation of the tangent to ${{(x+2)}^{2}}+{{(y-3)}^{2}}=25$ at the point $A$ $(-5,7)$ is $3x-4y+43=0$.
So the answer to the required equation is $3x-4y+43=0$.
Note: Be careful while working with modulus. While squaring a modulus, we can simply square the expression that’s present inside the modulus, rather than considering both the positive and negative possibilities of the expression. This is because whatever the expression is, the square of a negative number and a positive number of the same magnitude, are always equal. Thus, we can simply square the expression inside the modulus, without having to worry about the sign.
Last updated date: 24th Sep 2023
•
Total views: 362.4k
•
Views today: 7.62k
