Question

How do you find the exact values of the cot, cosec, and sec for 90 degrees?

Answer 1

Hint: The trigonometric ratios cot, cosec, and sec are the inverse functions of tan, sin, and cos respectively. Hence by finding the inverse of tan, sin, and cos, we can find out the exact values of the cot, cosec, and sec.

Complete Step by Step Solution:
Let us consider a unit circle whose radius is equal to one $\left( r=1 \right)$. At a point, ${{P}_{1}}$ the opposite side and the adjacent side of the angle will be equal to its projection on vertical and horizontal axes respectively.
When the line rotates to a point P shown in the figure (angle is 90 degrees), the opposite side will be equal to the radius of the circle, and the adjacent side will be equal to zero. We can also note that the hypotenuse is equal to the opposite side.

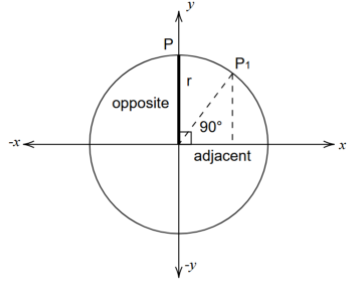
Since we have considered a unit circle, the opposite side and the hypotenuse will be equal to 1. We know that the cot, sec, and cosec are the inverse functions of tan, cos, and sin.
$\Rightarrow \cot \theta =\dfrac{1}{\tan \theta }$
$\Rightarrow \csc \theta =\dfrac{1}{\sin \theta }$ and
$\Rightarrow \sec \theta =\dfrac{1}{\cos \theta }$
Now let us find out the trigonometric ratios of sin, cos, and tan functions.
For 90 degrees, the sin value will be equal to
$\Rightarrow \sin \theta =\dfrac{\text{opposite side}}{\text{hypotenuse }}$
$\Rightarrow \sin {{90}^{\circ }}=\dfrac{1}{1}=1$ ……(1)
For 90 degrees, the cos value will be equal to
$\Rightarrow \cos \theta =\dfrac{\text{adjacent side}}{\text{hypotenuse}}$
$\Rightarrow \cos \theta =\dfrac{0}{1}=0$ ……(2)
For 90 degrees, the tan will be equal to
$\Rightarrow \tan {{90}^{\circ }}=\dfrac{\text{opposite side}}{\text{adjacent side}}$
$\Rightarrow \tan {{90}^{\circ }}=\dfrac{1}{0}=\infty $
$\Rightarrow \tan {{90}^{\circ }}=\text{Not defined}$ ……(3)
Using equations (1), (2), and (3), let us calculate cot, csc, and sec.
$\Rightarrow \cot {{90}^{\circ }}=\dfrac{1}{\tan {{90}^{\circ }}}=\dfrac{1}{\infty }$
Infinity is not a defined number and so a number divided by infinity is also undefined.

$\Rightarrow \cot {{90}^{\circ }}=\text{Not defined}$
Similarly
$\Rightarrow \csc {{90}^{\circ }}=\dfrac{1}{\sin {{90}^{\circ }}}=\dfrac{1}{1}=1$
$\Rightarrow \sec {{90}^{\circ }}=\dfrac{1}{\cos {{90}^{\circ }}}=\dfrac{1}{0}=\infty $ (Not defined)

Note:
In mathematics, infinity is used to denote an uncountably large number. This is a conceptual quantity and so it cannot be defined. Hence $\tan {{90}^{\circ }}$, $\cot {{90}^{\circ }}$, and $\sec {{90}^{\circ }}$are undefinable ratios. We cannot find the exact numerical values of these ratios.