Question

Find the factors of 330.
A. $$2\times 4\times 5\times 11$$
B. $$2\times 3\times 7\times 13$$
C. $$2\times 3\times 5\times 13$$
D. $$2\times 3\times 5\times 11$$

Answer 1

Hint: Here, we will find the factors of the given number using the concept of prime factorization. Prime factorization is a method in which a number is factorized to get factors as prime numbers. Factors are defined as the whole number multiplied by a number to get another number.

Complete step-by-step answer:
We are given a number 330.
We will find the factors of 330 by using the method of prime factorization.
We will follow the following steps has to perform doing prime factorization:
First, we will divide the number by the smallest prime number which divides the number exactly.
We will divide the quotient again by the smallest or the next smallest prime number if it is not exactly divisible by the smallest prime number.
We divide the process again and again till the quotient becomes 1.
We multiply the factors.
So, using the steps, we get

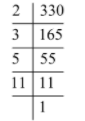
Thus, the factors of 330 are 2, 3, 5, and 11. As the factors are prime numbers, therefore we cannot factorize it further.
Therefore, the factors of 330 are $$2\times 3\times 5\times 11$$.

Note: We should remember that we should use only the prime factors. the product should be the number itself. We can also use the factor tree method.

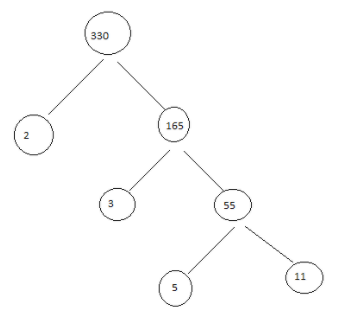
In factor tree method, the given number has to be multiplied by a prime factor and a composite factor. The composite factor has to be factorized by a prime factor and a composite factor. This has to be continued till all the factors become the prime factors. Each number is a factor of itself and The number 1 is a factor of every number. Thus the number 1 can be neglected. The product should be the number itself. Thus the numbers become the factors.