Find the foot of perpendicular and image of point $\left( {1,2,1} \right)$ along the line $\dfrac{{x - 3}}{1} = \dfrac{{y + 1}}{2} = \dfrac{{z - 1}}{3} = \lambda $.
Answer
Verified538.5k+ views
Hint: Here,we will draw a figure representing this situation. Then, we will find the direction ratios of the line. As both the lines are perpendicular to each other, we will be able to find the value of $\lambda $. Using this we will find the required coordinates of the foot of the perpendicular which could be used as a midpoint to find the coordinates of the image of the given point.
Formula Used:
We will use the following formulas:
1. If an equation of a line is given by $\dfrac{{x - a}}{d} = \dfrac{{y - b}}{e} = \dfrac{{z - c}}{f} = k$.
Then, $\left( {d,e,f} \right)$ represents the direction ratios of the given line
2. The direction ratios of a line passing through two points $\left( {p,q,r} \right)$ and $\left( {x,y,z} \right)$ is given by $\left( {x - p,y - q,z - r} \right)$.
3. If two lines are perpendicular to each other, then, the sum of product of their direction ratios is 0.
4. Coordinates of the mid-point $Q$ is given as $\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2},\dfrac{{{z_1} + {z_2}}}{2}$.
Complete step-by-step answer:
Given equation of line is $\dfrac{{x - 3}}{1} = \dfrac{{y + 1}}{2} = \dfrac{{z - 1}}{3} = \lambda $
Now, we will cross multiply to find the respective values of $x,y,z$
Hence, we get,
$x = \lambda + 3$
$y = 2\lambda - 1$
$z = 3\lambda + 1$
Now, the direction ratios of the given line are: $\left( {1,2,3} \right)$ because if an equation of a line is given by
$\dfrac{{x - a}}{d} = \dfrac{{y - b}}{e} = \dfrac{{z - c}}{f} = k$
Then, $\left( {d,e,f} \right)$ represents the direction ratios of the given line
Now, we will draw a figure representing the given situation.
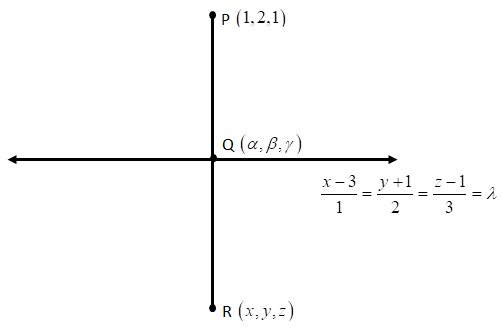
Now, let the coordinates of the foot of perpendicular line of the given line be $Q = \left( {\alpha ,\beta ,\gamma } \right)$
Since this foot of perpendicular lies on both the lines as it is their point of intersection.
Thus, it will satisfy the given equation of the line.
Hence, substituting $\left( {x,y,z} \right) = \left( {\alpha ,\beta ,\gamma } \right)$ in the equation of the line and after cross multiplying, we get,
$\alpha = \lambda + 3$
$\beta = 2\lambda - 1$
$\lambda = 3\lambda + 1$………………………………….$\left( 1 \right)$
Now, the direction ratios of a line passing through two points $\left( {p,q,r} \right)$ and $\left( {x,y,z} \right)$ is given by $\left( {x - p,y - q,z - r} \right)$
Since, the perpendicular line consists of the given point $M\left( {1,2,1} \right)$ and it also passes through the foot of perpendicular $Q = \left( {\alpha ,\beta ,\gamma } \right)$
Hence, the direction ratios of the perpendicular line are: $\left( {\alpha - 1,\beta - 2,\gamma - 1} \right)$
Now, using the fact that if two lines are perpendicular to each other, then, the sum of product of their direction ratios is 0, we get,
$1\left( {\alpha - 1} \right) + 2\left( {\beta - 2} \right) + \left( 3 \right)\left( {\gamma - 1} \right) = 0$
$ \Rightarrow \alpha - 1 + 2\beta - 4 + 3\gamma - 3 = 0$
Here, substituting the values of $\left( {\alpha ,\beta ,\gamma } \right)$ from $\left( 1 \right)$, we get,
$ \Rightarrow \lambda + 3 - 1 + 2\left( {2\lambda - 1} \right) - 4 + 3\left( {3\lambda + 1} \right) - 3 = 0$
$ \Rightarrow \lambda + 2 + 4\lambda - 2 - 4 + 9\lambda + 3 - 3 = 0$
Solving further, we get,
$ \Rightarrow 14\lambda - 4 = 0$
Dividing both sides by 2
$ \Rightarrow 7\lambda - 2 = 0$
Adding 2 on both sides
$ \Rightarrow 7\lambda = 2$
And, dividing both sides by 7, we get,
$ \Rightarrow \lambda = \dfrac{2}{7}$
Substituting this value in $\left( 1 \right)$, we get,
$\alpha = \dfrac{2}{7} + 3 = \dfrac{{23}}{7}$
$\beta = 2\left( {\dfrac{2}{7}} \right) - 1 = = \dfrac{4}{7} - 1 = \dfrac{{ - 3}}{7}$
$\lambda = 3\left( {\dfrac{4}{7}} \right) + 1 = \dfrac{{12}}{7} + 1 = \dfrac{{19}}{7}$
Therefore, the coordinates of foot of perpendicular are $\left( {\alpha ,\beta ,\gamma } \right) = \left( {\dfrac{{23}}{7},\dfrac{{ - 3}}{7},\dfrac{{19}}{7}} \right)$
Now, if the coordinates of the image of the given point is $R = \left( {x,y,z} \right)$
Then, we know that the foot of perpendicular should be the midpoint of the perpendicular line $PR$.
Hence, coordinates of the mid-point $Q$ will be:
$\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2},\dfrac{{{z_1} + {z_2}}}{2}$
Here, substituting $\left( {{x_1},{y_1},{z_1}} \right) = \left( {1,2,1} \right)$ and $\left( {{x_2},{y_2},{z_2}} \right) = \left( {x,y,z} \right)$
$ \Rightarrow $ Coordinates of the mid-point $Q$ will be $\dfrac{{1 + x}}{2},\dfrac{{2 + y}}{2},\dfrac{{1 + z}}{2}$
But, the coordinates of foot of perpendicular $Q = \left( {\dfrac{{23}}{7},\dfrac{{ - 3}}{7},\dfrac{{19}}{7}} \right)$
Hence, we get,
$\left( {\dfrac{{23}}{7},\dfrac{{ - 3}}{7},\dfrac{{19}}{7}} \right) = \left( {\dfrac{{1 + x}}{2},\dfrac{{2 + y}}{2},\dfrac{{1 + z}}{2}} \right)$
After comparing, we get,
$\dfrac{{23}}{7} = \dfrac{{1 + x}}{2}$
$ \Rightarrow 7x + 7 = 46$
Subtracting 7 from both sides, we get
$ \Rightarrow 7x = 39$
Dividing both sides by 7, we get
$ \Rightarrow x = \dfrac{{39}}{7}$
Similarly,
$\dfrac{{ - 3}}{7} = \dfrac{{2 + y}}{2}$
$ \Rightarrow 7y + 14 = - 6$
Subtracting 14 from both sides, we get
$ \Rightarrow 7y = - 20$
Dividing both sides by 7, we get
$ \Rightarrow y = \dfrac{{ - 20}}{7}$
Also,
$\dfrac{{19}}{7} = \dfrac{{1 + z}}{2}$
$ \Rightarrow 7z + 7 = 38$
Subtracting 7 from both sides, we get
$ \Rightarrow 7z = 31$
Dividing both sides by 7, we get
$ \Rightarrow z = \dfrac{{31}}{7}$
Therefore, the coordinates of the image of the given point $R = \left( {\dfrac{{39}}{7},\dfrac{{ - 20}}{7},\dfrac{{31}}{7}} \right)$
Hence, the foot of perpendicular and image of point $\left( {1,2,1} \right)$ along the line $\dfrac{{x - 3}}{1} = \dfrac{{y + 1}}{2} = \dfrac{{z - 1}}{3} = \lambda $ are $\left( {\dfrac{{23}}{7},\dfrac{{ - 3}}{7},\dfrac{{19}}{7}} \right)$ and $\left( {\dfrac{{39}}{7},\dfrac{{ - 20}}{7},\dfrac{{31}}{7}} \right)$ respectively.
Thus, this is the required answer.
Note:
When two lines meet or intersect each other at right angles or 90 degrees, they are said to be perpendicular to each other. Now, when a point is being reflected on a mirror or a line then, the distance of the point from the line is equal to the distance of its image behind the line. Thus, the point of intersection or the foot of perpendicular turns out to be the midpoint of the line. Hence, these facts about reflection should be kept in mind while solving these types of questions.
Formula Used:
We will use the following formulas:
1. If an equation of a line is given by $\dfrac{{x - a}}{d} = \dfrac{{y - b}}{e} = \dfrac{{z - c}}{f} = k$.
Then, $\left( {d,e,f} \right)$ represents the direction ratios of the given line
2. The direction ratios of a line passing through two points $\left( {p,q,r} \right)$ and $\left( {x,y,z} \right)$ is given by $\left( {x - p,y - q,z - r} \right)$.
3. If two lines are perpendicular to each other, then, the sum of product of their direction ratios is 0.
4. Coordinates of the mid-point $Q$ is given as $\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2},\dfrac{{{z_1} + {z_2}}}{2}$.
Complete step-by-step answer:
Given equation of line is $\dfrac{{x - 3}}{1} = \dfrac{{y + 1}}{2} = \dfrac{{z - 1}}{3} = \lambda $
Now, we will cross multiply to find the respective values of $x,y,z$
Hence, we get,
$x = \lambda + 3$
$y = 2\lambda - 1$
$z = 3\lambda + 1$
Now, the direction ratios of the given line are: $\left( {1,2,3} \right)$ because if an equation of a line is given by
$\dfrac{{x - a}}{d} = \dfrac{{y - b}}{e} = \dfrac{{z - c}}{f} = k$
Then, $\left( {d,e,f} \right)$ represents the direction ratios of the given line
Now, we will draw a figure representing the given situation.
Now, let the coordinates of the foot of perpendicular line of the given line be $Q = \left( {\alpha ,\beta ,\gamma } \right)$
Since this foot of perpendicular lies on both the lines as it is their point of intersection.
Thus, it will satisfy the given equation of the line.
Hence, substituting $\left( {x,y,z} \right) = \left( {\alpha ,\beta ,\gamma } \right)$ in the equation of the line and after cross multiplying, we get,
$\alpha = \lambda + 3$
$\beta = 2\lambda - 1$
$\lambda = 3\lambda + 1$………………………………….$\left( 1 \right)$
Now, the direction ratios of a line passing through two points $\left( {p,q,r} \right)$ and $\left( {x,y,z} \right)$ is given by $\left( {x - p,y - q,z - r} \right)$
Since, the perpendicular line consists of the given point $M\left( {1,2,1} \right)$ and it also passes through the foot of perpendicular $Q = \left( {\alpha ,\beta ,\gamma } \right)$
Hence, the direction ratios of the perpendicular line are: $\left( {\alpha - 1,\beta - 2,\gamma - 1} \right)$
Now, using the fact that if two lines are perpendicular to each other, then, the sum of product of their direction ratios is 0, we get,
$1\left( {\alpha - 1} \right) + 2\left( {\beta - 2} \right) + \left( 3 \right)\left( {\gamma - 1} \right) = 0$
$ \Rightarrow \alpha - 1 + 2\beta - 4 + 3\gamma - 3 = 0$
Here, substituting the values of $\left( {\alpha ,\beta ,\gamma } \right)$ from $\left( 1 \right)$, we get,
$ \Rightarrow \lambda + 3 - 1 + 2\left( {2\lambda - 1} \right) - 4 + 3\left( {3\lambda + 1} \right) - 3 = 0$
$ \Rightarrow \lambda + 2 + 4\lambda - 2 - 4 + 9\lambda + 3 - 3 = 0$
Solving further, we get,
$ \Rightarrow 14\lambda - 4 = 0$
Dividing both sides by 2
$ \Rightarrow 7\lambda - 2 = 0$
Adding 2 on both sides
$ \Rightarrow 7\lambda = 2$
And, dividing both sides by 7, we get,
$ \Rightarrow \lambda = \dfrac{2}{7}$
Substituting this value in $\left( 1 \right)$, we get,
$\alpha = \dfrac{2}{7} + 3 = \dfrac{{23}}{7}$
$\beta = 2\left( {\dfrac{2}{7}} \right) - 1 = = \dfrac{4}{7} - 1 = \dfrac{{ - 3}}{7}$
$\lambda = 3\left( {\dfrac{4}{7}} \right) + 1 = \dfrac{{12}}{7} + 1 = \dfrac{{19}}{7}$
Therefore, the coordinates of foot of perpendicular are $\left( {\alpha ,\beta ,\gamma } \right) = \left( {\dfrac{{23}}{7},\dfrac{{ - 3}}{7},\dfrac{{19}}{7}} \right)$
Now, if the coordinates of the image of the given point is $R = \left( {x,y,z} \right)$
Then, we know that the foot of perpendicular should be the midpoint of the perpendicular line $PR$.
Hence, coordinates of the mid-point $Q$ will be:
$\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2},\dfrac{{{z_1} + {z_2}}}{2}$
Here, substituting $\left( {{x_1},{y_1},{z_1}} \right) = \left( {1,2,1} \right)$ and $\left( {{x_2},{y_2},{z_2}} \right) = \left( {x,y,z} \right)$
$ \Rightarrow $ Coordinates of the mid-point $Q$ will be $\dfrac{{1 + x}}{2},\dfrac{{2 + y}}{2},\dfrac{{1 + z}}{2}$
But, the coordinates of foot of perpendicular $Q = \left( {\dfrac{{23}}{7},\dfrac{{ - 3}}{7},\dfrac{{19}}{7}} \right)$
Hence, we get,
$\left( {\dfrac{{23}}{7},\dfrac{{ - 3}}{7},\dfrac{{19}}{7}} \right) = \left( {\dfrac{{1 + x}}{2},\dfrac{{2 + y}}{2},\dfrac{{1 + z}}{2}} \right)$
After comparing, we get,
$\dfrac{{23}}{7} = \dfrac{{1 + x}}{2}$
$ \Rightarrow 7x + 7 = 46$
Subtracting 7 from both sides, we get
$ \Rightarrow 7x = 39$
Dividing both sides by 7, we get
$ \Rightarrow x = \dfrac{{39}}{7}$
Similarly,
$\dfrac{{ - 3}}{7} = \dfrac{{2 + y}}{2}$
$ \Rightarrow 7y + 14 = - 6$
Subtracting 14 from both sides, we get
$ \Rightarrow 7y = - 20$
Dividing both sides by 7, we get
$ \Rightarrow y = \dfrac{{ - 20}}{7}$
Also,
$\dfrac{{19}}{7} = \dfrac{{1 + z}}{2}$
$ \Rightarrow 7z + 7 = 38$
Subtracting 7 from both sides, we get
$ \Rightarrow 7z = 31$
Dividing both sides by 7, we get
$ \Rightarrow z = \dfrac{{31}}{7}$
Therefore, the coordinates of the image of the given point $R = \left( {\dfrac{{39}}{7},\dfrac{{ - 20}}{7},\dfrac{{31}}{7}} \right)$
Hence, the foot of perpendicular and image of point $\left( {1,2,1} \right)$ along the line $\dfrac{{x - 3}}{1} = \dfrac{{y + 1}}{2} = \dfrac{{z - 1}}{3} = \lambda $ are $\left( {\dfrac{{23}}{7},\dfrac{{ - 3}}{7},\dfrac{{19}}{7}} \right)$ and $\left( {\dfrac{{39}}{7},\dfrac{{ - 20}}{7},\dfrac{{31}}{7}} \right)$ respectively.
Thus, this is the required answer.
Note:
When two lines meet or intersect each other at right angles or 90 degrees, they are said to be perpendicular to each other. Now, when a point is being reflected on a mirror or a line then, the distance of the point from the line is equal to the distance of its image behind the line. Thus, the point of intersection or the foot of perpendicular turns out to be the midpoint of the line. Hence, these facts about reflection should be kept in mind while solving these types of questions.
Recently Updated Pages
A man running at a speed 5 ms is viewed in the side class 12 physics CBSE
The number of solutions in x in 02pi for which sqrt class 12 maths CBSE
State and explain Hardy Weinbergs Principle class 12 biology CBSE
Write any two methods of preparation of phenol Give class 12 chemistry CBSE
Which of the following statements is wrong a Amnion class 12 biology CBSE
Differentiate between action potential and resting class 12 biology CBSE
Trending doubts
What are the major means of transport Explain each class 12 social science CBSE
Which are the Top 10 Largest Countries of the World?
Draw a labelled sketch of the human eye class 12 physics CBSE
How much time does it take to bleed after eating p class 12 biology CBSE
Explain sex determination in humans with line diag class 12 biology CBSE
Explain sex determination in humans with the help of class 12 biology CBSE