Question

Find the foot of the perpendicular and the image of the point (1,2,1) along the line
$\dfrac{x-1}{1}=\dfrac{y+1}{2}=\dfrac{z-1}{3}=\lambda $

Answer 1

Hint: In this question, we are given the equation of the line and the coordinates of the point. As the foot of the perpendicular must lie on the line, we should use the relation direction ratios of the perpendicular and that of the line to obtain the point of intersection. Then, as the point of intersection should be the midpoint of the original point and its image, we can use the equation for midpoint to find the coordinates of the image of the point.

Complete step by step solution:
We know that the direction ratios of a line represented by
$\dfrac{x-a}{d}=\dfrac{x-b}{e}=\dfrac{x-c}{f}=k$
Is given by (d,e,f). In this case, the given equation of the line is
$\dfrac{x-1}{1}=\dfrac{y+1}{2}=\dfrac{z-1}{3}=\lambda .................(1.1)$
Therefore, the direction ratios of the line are (1,2,3) ………………………… (1.2)
Now, we can rewrite the three equations in (1.1) as
$\begin{align}
  & x-1=\lambda \\
 & y+1=2\lambda \\
 & z-1=3\lambda .............................(1.3) \\
\end{align}$
Let the coordinates of the foot of the perpendicular be $Q=\left( \alpha ,\beta ,\gamma \right)$ as shown in the figure.

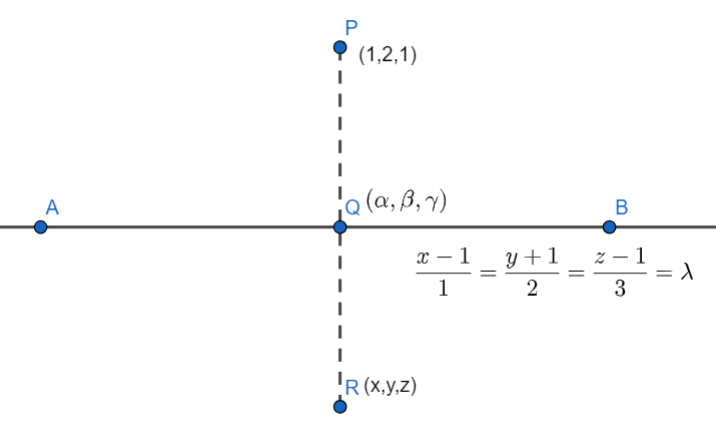
As the foot of the perpendicular should lie on the given line, $\left( \alpha ,\beta ,\gamma \right)$ should satisfy equation (1.3), therefore, we should have
$\begin{align}
  & \alpha -1=\lambda \Rightarrow \alpha =1+\lambda \\
 & \beta +1=2\lambda \Rightarrow \beta =2\lambda -1 \\
 & \gamma -1=3\lambda \Rightarrow \gamma =3\lambda +1.............................(1.4) \\
\end{align}$
The direction ratios of a line passing through two points (p,q,r) and (s,t,u) is given by (s-p, t-q,u-r). Now, the perpendicular line starts from $P=(1,2,1)$ and passes through $Q=\left( \alpha ,\beta ,\gamma \right)$, therefore the direction ratios of the perpendicular line PQ should be $\left( \alpha -1,\beta -2,\gamma -1 \right)$……..(1.5)
We know that if two lines having direction ratios $\left( a,b,c \right)$ and $\left( d,e,f \right)$ are perpendicular then
$ad+be+cf=0..............(1.6)$
Thus, as PQ should be perpendicular to the given line, using equations (1.6), (1.5) and (1.2), we get
$\left( \alpha -1 \right)\times 1+\left( \beta -2 \right)\times 2+\left( \gamma -1 \right)\times 3=0...........(1.7a)$
Now, using the values from equation (1.4), we get
$\begin{align}
  & \lambda \times 1+\left( 2\lambda -3 \right)\times 2+3\lambda \times 3=0 \\
 & \Rightarrow 14\lambda =6\Rightarrow \lambda =\dfrac{6}{14}=\dfrac{3}{7}................(1.7) \\
\end{align}$
So, using this values of $\lambda $ in equation (1.4), we get
\[\begin{align}
  & \alpha =1+\lambda =1+\dfrac{3}{7}=\dfrac{10}{7} \\
 & \beta =2\lambda -1=2\times \dfrac{3}{7}-1=\dfrac{-1}{7} \\
 & \gamma =3\lambda +1=3\times \dfrac{3}{7}+1=\dfrac{16}{7}.............................(1.8) \\
\end{align}\]
Thus, from equation (1.8), we obtain the coordinates of the foot of the perpendicular to be $\left( \dfrac{10}{7},\dfrac{-1}{7},\dfrac{16}{7} \right)..................(1.9)$
Now, if the coordinates of the image R is $\left( x,y,z \right)$, then we know that the foot of the perpendicular should be the midpoint of the line PR. Therefore, as the coordinates of the midpoint Q should be average of the coordinates of the end points P and R, from equations (1.9) and the coordinates of the given point (1,2,1), we obtain
$\begin{align}
  & \dfrac{10}{7}=\dfrac{1+x}{2}\Rightarrow x=\dfrac{20}{7}-1=\dfrac{13}{7} \\
 & \dfrac{-1}{7}=\dfrac{2+y}{2}\Rightarrow y=\dfrac{-2}{7}-2=\dfrac{-16}{7} \\
 & \dfrac{16}{7}=\dfrac{1+z}{2}\Rightarrow z=\dfrac{16}{7}-1=\dfrac{9}{7} \\
\end{align}$
Thus, the coordinates of the image should be $\left( \dfrac{13}{7},\dfrac{-16}{7},\dfrac{9}{7} \right).................(1.10)$
Therefore, equations (1.9) and (1.10) are the required answer to the given question.

Note: We should note that in equation (1.5), we could also have written the direction ratios of PQ as $\left( 1-\alpha ,2-\beta ,1-\gamma \right)$ by interchanging the order in which P and Q are taken while finding the direction ratios, however the answer would still remain the same as in this case only an overall minus sign will be introduce in (1.7a) which will get cancelled out as the RHS is zero.