Question

Find the foot of the perpendicular from point$(2,3,2)$to the line$\dfrac{{4 - x}}{2} = \dfrac{y}{6} = \dfrac{{1 - z}}{3}$. Also find the perpendicular distance from the point to the line.

Answer 1

Hint: The equation of the given line is its Cartesian equation. Let O be the foot of the perpendicular. Let$\dfrac{{x - 4}}{{ - 2}} = \dfrac{{y - 0}}{6} = \dfrac{{z - 1}}{{ - 3}} = k$. Use this to compute the direct ratio of the perpendicular.
Use the direction ratios of the given line and the fact that its dot product with the direction ratio of the perpendicular will be 0 to find the coordinates of O. Now, use the distance formula \[d = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2} + {{({z_2} - {z_1})}^2}} \]to find the perpendicular distance between $(2,3,2)$and O.

Complete step by step solution:
Given an equation of a line$\dfrac{{4 - x}}{2} = \dfrac{y}{6} = \dfrac{{1 - z}}{3}$and a point$(2,3,2)$
Let us look at the diagrammatic representation of this problem.
Let$P \equiv (2,3,2)$and AB be the line represented by the equation$\dfrac{{4 - x}}{2} = \dfrac{y}{6} = \dfrac{{1 - z}}{3}$.
Also, let O be the foot of the perpendicular drawn from point P to the line AB.
Thus, we get the following picture:

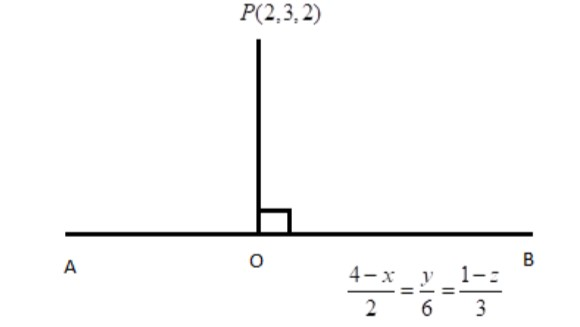
There are two parts to the given question.
1) Finding the foot of the perpendicular - as per the diagram this would mean we need to find the coordinates of the point O.
2) Finding the perpendicular distance - as per the diagram this means finding the length of PO.
Rearrange the terms in the numerator of $\dfrac{{4 - x}}{2} = \dfrac{y}{6} = \dfrac{{1 - z}}{3}$to obtain the Cartesian equation of the line.
Therefore, we get
$\dfrac{{x - 4}}{{ - 2}} = \dfrac{{y - 0}}{6} = \dfrac{{z - 1}}{{ - 3}}$
This is the Cartesian equation of the line passing through the point$(4,0,1)$with direction ratios -2, 6, and -3.
Now, let $O \equiv (x,y,z)$
We will use the above Cartesian equation to obtain the coordinates of the point O.
Let$\dfrac{{x - 4}}{{ - 2}} = \dfrac{{y - 0}}{6} = \dfrac{{z - 1}}{{ - 3}} = k$
Then, we have for any point$(x,y,z)$on the line AB:
$
  x - 4 = - 2k \\
  y = 6k \\
  z - 1 = - 3k \\
 $
This implies that$x = 4 - 2k,y = 6k,z = 1 - 3k$
Therefore, we have$O \equiv (x = 4 - 2k,y = 6k,z = 1 - 3k)$
Now we will use the formula of direction ratios of the line joining two points, say,$P(a,b,c)$and$Q(d,e,f)$
Thus, the direction ratios are taken as$(a - d,b - e,c - f)$or$(d - a,e - b,f - c)$
Consider the direction ratios of the points$O \equiv (x = 4 - 2k,y = 6k,z = 1 - 3k)$and$P \equiv (2,3,2)$.
Thus, we get the direction ratios as\[\overline {OP} \equiv (4 - 2k - 2,6k - 3,1 - 3k - 2) = (2 - 2k,6k - 3, - 1 - 3k)\]
Also, we have the direction ratios of the line$\dfrac{{4 - x}}{2} = \dfrac{y}{6} = \dfrac{{1 - z}}{3}$given by$\overline {AB} = ( - 2,6, - 3)$.
As OP is perpendicular to the line AB, we know that$\overline {OP} \cdot \overline {AB} = 0$
Now, $\overline {OP} \cdot \overline {AB} = 0$implies that
\[
  (2 - 2k,6k - 3, - 1 - 3k) \cdot ( - 2,6, - 3) = 0 \\
   \Rightarrow (2 - 2k)( - 2) + (6k - 3)6 + ( - 1 - 3k)( - 3) = 0 \\
   \Rightarrow - 4 + 4k + 36k - 18 + 3 + 9k = 0 \\
   \Rightarrow 49k - 19 = 0 \\
   \Rightarrow k = \dfrac{{19}}{{49}} \\
 \]
Therefore, we have
$
  O \equiv (x = 4 - 2k,y = 6k,z = 1 - 3k) \\
   \equiv (x = 4 - 2(\dfrac{{19}}{{49}}),y = 6(\dfrac{{19}}{{49}}),z = 1 - 3(\dfrac{{19}}{{49}})) \\
   \equiv (x = 4 - \dfrac{{38}}{{49}},y = \dfrac{{114}}{{49}},z = 1 - \dfrac{{57}}{{49}}) \\
   \equiv (\dfrac{{158}}{{49}},\dfrac{{114}}{{49}}, - \dfrac{8}{{49}}) \\
 $
This answers the first part of the question. We now have the foot of the perpendicular which is$(\dfrac{{158}}{{49}},\dfrac{{114}}{{49}}, - \dfrac{8}{{49}})$.
To answer the second part, we will only need the distance formula for two points.
The distance between two points (x1, y1, z1) and (x2, y2, z2) is denoted by d and is given by the formula
\[d = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2} + {{({z_2} - {z_1})}^2}} \]
Therefore, length of PO is given by
\[
  d = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2} + {{({z_2} - {z_1})}^2}} \\
   = \sqrt {{{(2 - \dfrac{{158}}{{49}})}^2} + {{(3 - \dfrac{{114}}{{49}})}^2} + {{(2 - \dfrac{{( - 8)}}{{49}})}^2}} \\
   = \sqrt {{{(\dfrac{{60}}{{49}})}^2} + {{(\dfrac{{33}}{{49}})}^2} + {{(\dfrac{{106}}{{49}})}^2}} \\
   = \dfrac{{\sqrt {15,925} }}{{49}} \\
 \]
Hence the required answers are$(\dfrac{{158}}{{49}},\dfrac{{114}}{{49}}, - \dfrac{8}{{49}})$and\[\dfrac{{\sqrt {15,925} }}{{49}}\].
Note: It is advisable to be careful while using the distance formula. Some students make substitution errors and end up with the wrong answers. In this case, the point O has 3 coordinates, therefore, we modified the distance formula such that we could compute the distance between 2 points with 3 coordinates. This is an important step.