Question

Find the fringe width of the fringe pattern. (Assume the wavelength of the light used to be 500nm)

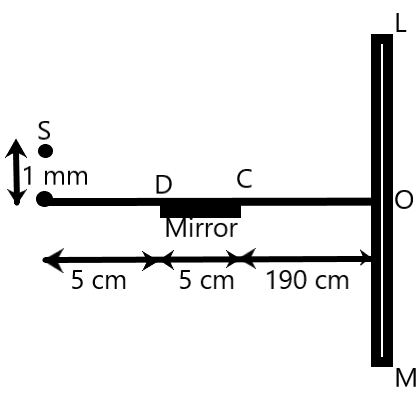
A) 0.05cm
B) 0.25cm
C) 0.01cm
D) 0.1cm

Answer 1

Hint: We are given a system in which a source, a slit, a mirror, and a screen. We need to find the fringe width of the fringes formed by this system which can be easily calculated by using Young’s double-slit experiment approach to this.

Complete step by step solution:
We know that Young’s double-slit experiment involves a pair of sources of coherent waves, which interfere at a point on the given screen to form the fringes. Here, we are given only one source and instead of a second source, a mirror has been installed in the path of the light.
We know that light rays from a source when falling on the mirror reflects and takes a different path. If we extend this path, we will get a point S’ which is a mirror image of the actual slit S. This slit S’ will be the virtual second source for our modified version of Young’s Double Slit Experiment. The highlighted colors in the figure show the extended rays.
We understand that now we can consider this as Young’s double-slit experiment for further calculation.

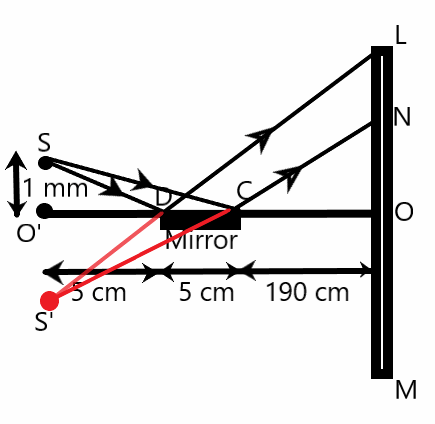
We need to find the fringe width of the interference pattern formed by this system. We know that the fringe width is independent of the fringe number. It only depends on the wavelength of the light, the distance D from the screen to the slits, and the slit width d.
i.e.,
The fringe width is given as –
\[\beta =\dfrac{\lambda D}{d}\]
We can find the fringe width as –
\[\begin{align}
  & \beta =\dfrac{\lambda D}{d} \\
 & \lambda =500\times {{10}^{-9}}m \\
 & D=2m \\
 & d=2\times {{10}^{-3}}m \\
 & \Rightarrow \beta =\dfrac{500\times {{10}^{-9}}\times 2}{2\times {{10}^{-3}}} \\
 & \therefore \beta =0.05cm \\
\end{align}\]
The fringe width of the given arrangement will be 0.05cm.
The correct answer is option A.

Note: The Young’s Double Slit experiment can be manipulated in any way such as to get two sources of coherent waves. The fringe width in a given setup is highly dependent on the physical parameters like the distances involved. We should be careful about the arrangement.