Question

Find the half angular width of the central bright maximum in the Fraunhofer diffraction pattern of a slit of width $12 \times {10^5}{\text{ }}cm$ when the slit is illuminated by monochromatic light of wavelength $6000\,{A^o}$.
A. ${40^ \circ }$
B. ${45^ \circ }$
C. ${30^ \circ }$
D. ${60^ \circ }$

Answer 1

Hint:Diffraction of light is defined as the bending of light around corners such that it spreads out and illuminates areas where a shadow is expected. In general, it is hard to separate diffraction from interference since both occur simultaneously. The silver lining which we witness in the sky is caused due to diffraction of light.

Formula used:
According to Fraunhofer diffraction pattern, the half angular width of central bright maximum is given by,
$a\sin \theta = \lambda $
where $\theta $width of the slit, $\lambda = $wavelength of the light used and $\theta $ is the half angle.

Complete step by step answer:

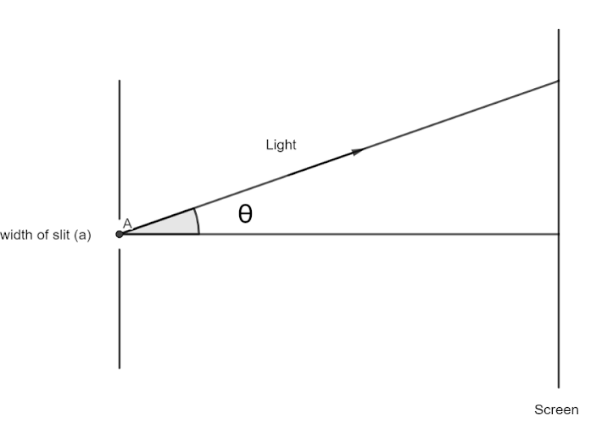
Here, it is mentioned in the question that the width of the slit is,
$a = $$12 \times {10^5}{\text{ }}cm$$ = 12 \times {10^{ - 7}}{\text{ }}m$
And the wavelength of the monochromatic light is given as,
$\lambda = 6000\,{A^o} = 6 \times {10^{ - 7}}{\text{ }}m$

Let us assume that the half angle is $\theta $. Now, By putting the values of $a$,$\lambda $ and $\theta $ to the Fraunhofer diffraction pattern’s formulae we get,
$a\sin \theta = \lambda \\
\Rightarrow \sin \theta = \dfrac{\lambda }{a} \\ $
Substituting the values of $\lambda $ and $a$ from the given question we get,
$\Rightarrow \sin \theta = \dfrac{{6000 \times {{10}^{ - 10}}}}{{12 \times {{10}^{ - 5}} \times {{10}^{ - 2}}}} \\
\Rightarrow \sin \theta = \dfrac{1}{2} \\
\Rightarrow \sin \theta = \sin {30^ \circ } \\ $
Now, cancelling out $\sin $ from both sides we get,
$ \therefore \theta = {30^ \circ }$
In this way we have easily found out that the half angular width of the central bright maximum in the Fraunhofer diffraction pattern is ${30^ \circ }$.

Thus, the correct option is C.

Note:We must know that this is the only formula to find out the half angular width of the central bright maximum. First of all we must convert every unit to SI units. Also if the width of the slit $a \gg \lambda $ then $\Delta \theta = 2\dfrac{\lambda }{a}$. In this way we could solve if the width of the slit is very greater than the wavelength of the light used. The formula used for the half angular fringe width in secondary maxima is $a\sin \theta = (2n + 1)\dfrac{\lambda }{2}$. The intensity is also maximum at the central bright fringe during a Fraunhofer diffraction of any light.