Question

Find the height of trapezium in which parallel sides are 25cm and 77cm and non-parallel sides are 26cm and 60cm. Given the area of trapezium as 1644$c{m^2}$.

Answer 1

Hint: In this question let h be the height of trapezium, by symmetry find the portion on side DC which is exactly same in length to AB (see figure), this divides the figure into three areas, that is a triangle ADE, a rectangle ABFE and another triangle BFC.

Complete step-by-step answer:

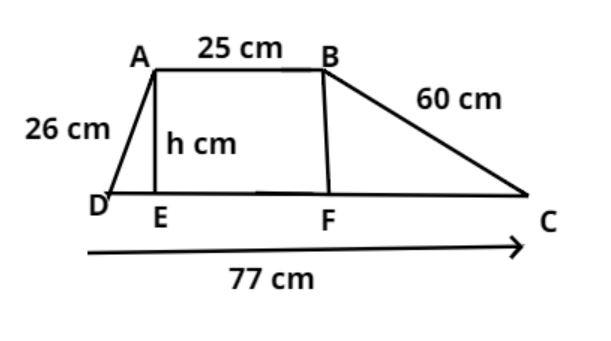
The pictorial representation of the trapezium ABCD is shown above.

Let AB and CD be the parallel sides and the length of the parallel sides are given which is
AB = 25 cm and CD = 77 cm.

And the length of non-parallel sides are

AD = 26 cm and BC = 60 cm.

Let AE and BF are the perpendiculars drawn on side CD respectively.

So by symmetry AB = EF = 25 cm

Let AE = BF = h cm.

And DE = x, FC = y cm.

Therefore from figure

DE + EF + FC = 77 cm.

$ \Rightarrow x + 25 + y = 77$

$ \Rightarrow x + y = 77 - 25 = 52$........................ (1)

Now as we know that the area of the triangle is half multiplied by base time’s perpendicular.

Therefore area of triangle ADE = $\dfrac{1}{2} \times x \times h$

And area of the triangle BFC = $\dfrac{1}{2} \times y \times h$

And area of rectangle ABEF = $\left( {25 \times h} \right)$

So the area (A) of trapezium = area of triangle ADE + area of triangle BFC + area of rectangle ABEF.

$ \Rightarrow A = \dfrac{1}{2} \times x \times h + \dfrac{1}{2} \times y \times h + \left( {25 \times h} \right)$

Now it is given that the area of trapezium is 1644 $cm^2$.

$ \Rightarrow 1644 = \dfrac{1}{2} \times h \times \left( {x + y} \right) + \left( {25 \times h} \right)$

Now from equation (1) we have,

$ \Rightarrow 1644 = \dfrac{1}{2} \times h \times \left( {52} \right) + \left( {25 \times h} \right) = 26h + 25h = 51h$

Therefore $h = \dfrac{{1644}}{{51}} = \dfrac{{548}}{{17}} = 32.24$ cm
So this is the required height of the trapezium.

Note: A trapezium is a quadrilateral with one pair of sides parallel. It is always advised to form diagrammatic representation using the information of the question as it helps understanding the geometry of the figure involved. Breaking down the total area into smaller areas of different shapes plays a key role in trapezium area related questions.