Question

Find the LCM of: 294, 420 and 504.

Answer 1

Hint: To find the LCM of the number first express the number into their products of prime numbers, then take the prime number with the highest power.

Complete step by step answer:
 First, find the prime factors of 294.
The prime factor of 294 is given below:

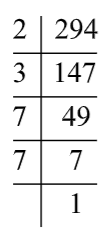
Express 294 as a product of their prime factors,
\[\begin{align}
  & 294=2\times 3\times 7\times 7 \\
 & 294=2\times 3\times {{7}^{2}} \\
\end{align}\] …… (1)

Now, find the prime factors of 420.
The prime factor of 420 is given below:

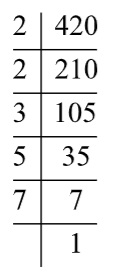
Express 420 as a product of their prime factors,
\[\begin{align}
  & 420=2\times 2\times 3\times 5\times 7 \\
 & 420={{2}^{2}}\times 3\times 5\times 7 \\
\end{align}\] …… (2)

Now, find the prime factors of 504.
The prime factor of 504 is given below:

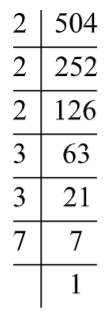
Express 504 as a product of their prime factors,
\[\begin{align}
  & 504=2\times 2\times 2\times 3\times 3\times 7 \\
 & 504={{2}^{3}}\times {{3}^{2}}\times 7 \\
\end{align}\] …… (3)
Now, from (1), (2) and (3) choose the prime number with greatest power and multiply them.
Therefore,
\[\begin{align}
  & LCM={{2}^{3}}\times {{3}^{2}}\times 5\times {{7}^{2}} \\
 & LCM=8\times 9\times 5\times 49 \\
 & LCM=17640 \\
\end{align}\]

Note: While choosing the prime numbers with greatest power make sure to choose every prime number even if some of it have power only one.