Question

Find the LCM of the following using prime factorization method: \[72,90,120.\]

Answer 1

Hint: LCM is elaborated as Least Common Multiple, which is the lowest common factor among the integers. To find the LCM of the given numbers, which is the lowest common number, which is divisible by all numbers for which we are finding the LCM, the method includes basic factorization of the numbers to find factors that are multiplied together to form a number. If the all given numbers are \[0\] for which LCM is being calculated, their LCM will also be \[0\]. First, find the factors of the number that are the number when multiplied together gives the original number.

Complete step by step answer:
To find the lowest common multiple of the numbers, let’s find the factors of the given numbers for which we have to find the LCM of each number \[72,90,120.\].
Factors are the integers, which, when multiplied together results in the original number only. First, find the factors of numbers.

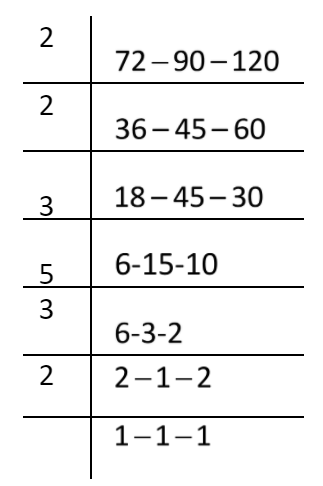
Now multiply the common multiple with the other factors of the LCM:
\[
  LCM = 2 \times 2 \times 3 \times 5 \times 3 \times 2 \\
   = 360 \\
 \]
Hence, the LCM of the numbers \[72,90,120\] is 360.

Note: LCM of given numbers is exactly divisible by each of the numbers. During the LCM calculation, students must know the tables of various numbers, and they have to perform the operations step by step. Lastly, they have to multiply all the numbers by which they are dividing the given set of numbers. The least common multiple, lowest common multiple, or smallest common multiple of two integers a and b, usually denoted by LCM (a, b), is the smallest positive integer that is divisible by both a and b.