Question

How do you find the length of the diagonal of a rectangle in terms of its base b and altitude h?

Answer 1

Hint: We start solving the problem by drawing the figure representing the given information by assuming vertices and length of diagonal of the rectangle. We then make use of the fact that the angles present in a rectangle are right angles to proceed through the problem. We then recall the Pythagoras theorem as the square of the hypotenuse is equal to the sum of the squares of the other two sides of the right-angle triangle to get the required answer.

Complete step by step answer:
According to the problem, we are asked to find the length of the diagonal of a rectangle in terms of its base b and altitude h.
Let us assume ABCD the rectangle with AB as base and BC as altitude. Now, let us assume that the length of the diagonal is ‘d’. Let us draw a figure representing this information.

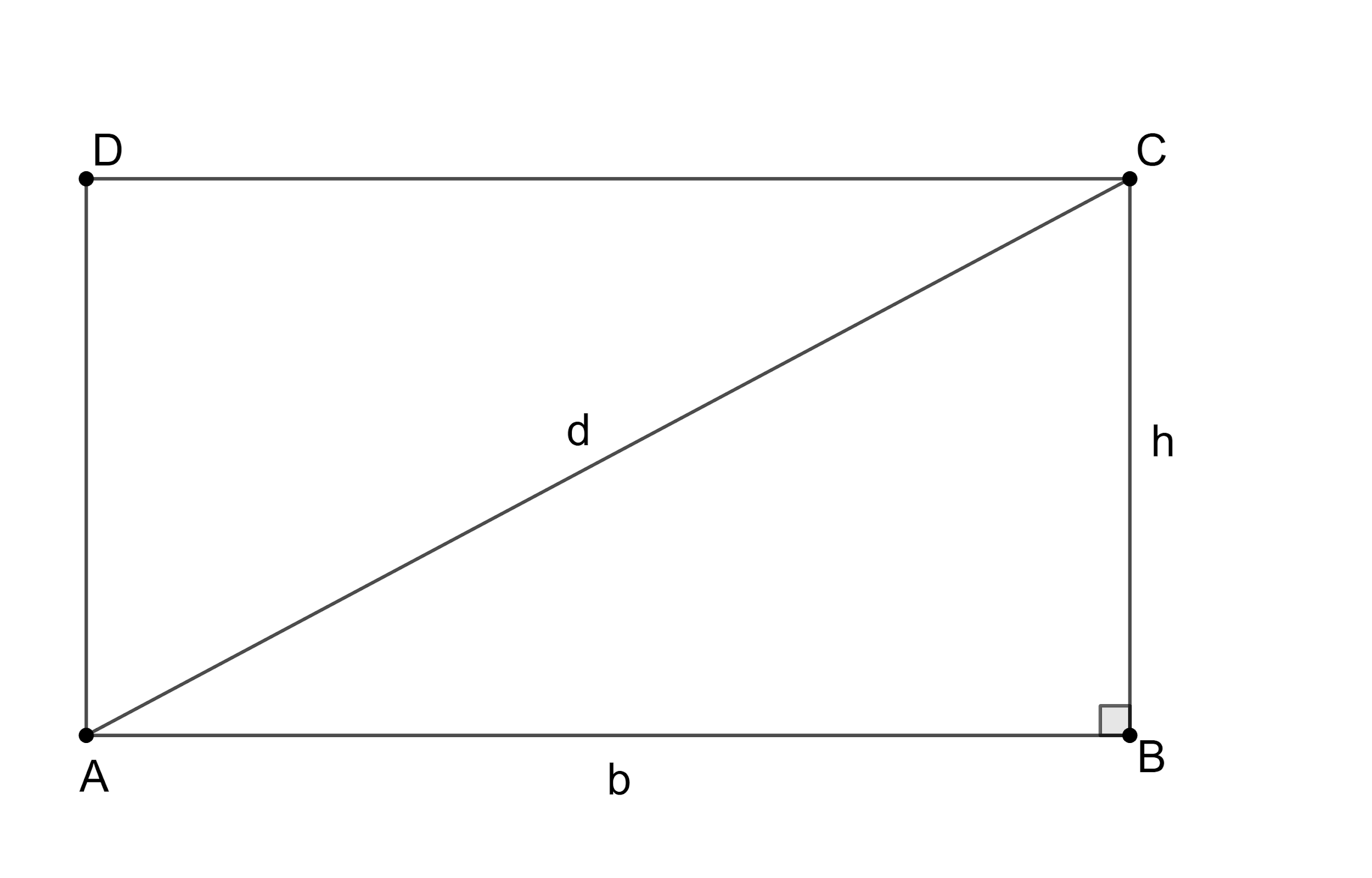
We know that the angles present in a rectangle are right angles.
From the figure, we can see that $ ABC $ is a right angle triangle with a right angle at B.
From Pythagoras theorem, we know that the square of the hypotenuse is equal to the sum of the squares of the other two sides of the right-angle triangle. We know that hypotenuse is the side opposite to the right angle in a right-angle triangle.
So, we get $ A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}} $ .
 $ \Rightarrow {{d}^{2}}={{b}^{2}}+{{h}^{2}} $ .
 $ \Rightarrow d=\sqrt{{{b}^{2}}+{{h}^{2}}} $ .
 $ \therefore $ We have found the length of the diagonal as $ \sqrt{{{b}^{2}}+{{h}^{2}}} $ .

Note: Whenever we get this type of problem, we first should draw the figure representing the given information to avoid confusion. We should not confuse the hypotenuse in a right angle triangle while solving this problem. We should keep in mind the angles at the vertices of the rectangle while solving this problem. Similarly, we can expect problems to find the length of the diagonal if its side is a.