Question

Find the locus of middle points of chords of an ellipse which subtend a right angle at center.

Answer 1

Hint:
In this question, we need to find a locus. For this, we will first write the standard equation of chord of contact when the middle point is given. Then we will form a homogeneous equation of ellipse with the help of chords to get the equation of lines passing through the center joining the point of contact. At last we will use the given condition to find required locus.

Complete step by step answer:
Here we are given an ellipse. Let us consider standard equation of ellipse as,
 $ \dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\cdots \cdots \cdots \left( 1 \right) $ .
Let us take a chord AB of ellipse having a middle point P(h,k) and subtending a right angle at the center of the ellipse. Our diagram looks like this,

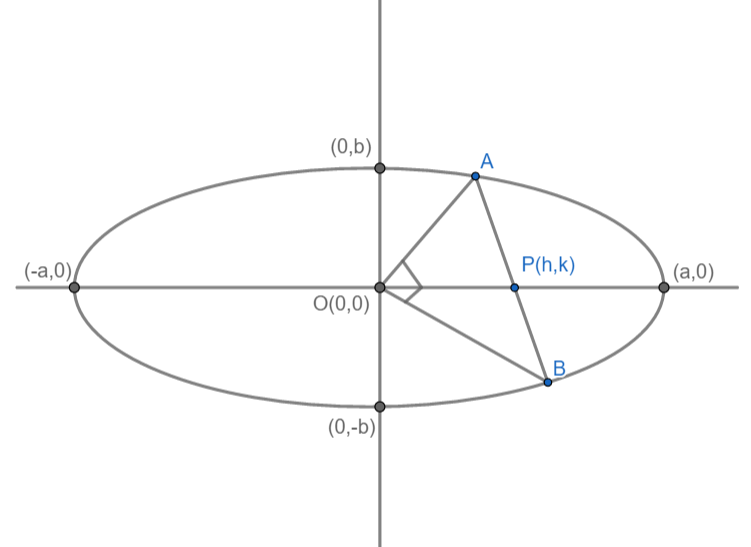
We know that equation of chord of contact when midpoint is given by, T = S'.
Where T is tangent equation w.r.t middle point.
T is found by replacing $ {{x}^{2}} $ by xx, $ {{y}^{2}} $ v by yy, x by $ \left( \dfrac{x+{{x}_{1}}}{2} \right) $ and y by $ \left( \dfrac{y+{{y}_{1}}}{2} \right) $ if middle point is $ \left( {{x}_{1}},{{y}_{1}} \right) $ .
S' is an equation of curve where $ x={{x}_{1}}\text{ and }y={{y}_{1}} $ .
So T can be written w.r.t middle point P(h,k) from equation of ellipse (1) as,
\[T=\dfrac{hx}{{{a}^{2}}}+\dfrac{ky}{{{b}^{2}}}-1\].
And S' will be $ \dfrac{{{h}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}}-1 $ .
So our equation of chord of contact become,
\[\dfrac{hx}{{{a}^{2}}}+\dfrac{ky}{{{b}^{2}}}-1=\dfrac{{{h}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}}-1\Rightarrow \dfrac{hx}{{{a}^{2}}}+\dfrac{ky}{{{b}^{2}}}=\dfrac{{{h}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}}\].
It can be written as,
\[\dfrac{\dfrac{hx}{{{a}^{2}}}+\dfrac{ky}{{{b}^{2}}}}{\dfrac{{{h}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}}}=1\cdots \cdots \cdots \left( 2 \right)\].
Now let us take the condition that the chord subtends $ {{90}^{\circ }} $ at origin.
We know that pair of straight lines passing through the origin (homogeneous equation) is given by,
 $ A{{X}^{2}}+2HXY+B{{Y}^{2}}=0 $ .
So let us convert the equation of ellipse and chord through extremities of which lines to origin are joined (AO and BO) into a homogeneous equation of the above form.
We have equation of ellipse as $ \dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1 $ which can be written as $ \dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}={{\left( 1 \right)}^{2}} $ .
Using the value of 1 from (2) in above equation we get,
 $ \dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}={{\left( \dfrac{\dfrac{hx}{{{a}^{2}}}+\dfrac{ky}{{{b}^{2}}}}{\dfrac{{{h}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}}} \right)}^{2}} $ .
Simplifying and cross multiplying we get,
\[\begin{align}
  & \left( \dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}} \right){{\left( \dfrac{{{h}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}} \right)}^{2}}={{\left( \dfrac{hx}{{{a}^{2}}}+\dfrac{ky}{{{b}^{2}}} \right)}^{2}} \\
 & \Rightarrow {{\left( \dfrac{{{h}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}} \right)}^{2}}\dfrac{{{x}^{2}}}{{{a}^{2}}}+{{\left( \dfrac{{{h}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}} \right)}^{2}}\dfrac{{{y}^{2}}}{{{b}^{2}}}={{\left( \dfrac{hx}{{{a}^{2}}}+\dfrac{ky}{{{b}^{2}}} \right)}^{2}} \\
\end{align}\].
Simplifying the right side we get,
\[\Rightarrow {{\left( \dfrac{{{h}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}} \right)}^{2}}\dfrac{{{x}^{2}}}{{{a}^{2}}}+{{\left( \dfrac{{{h}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}} \right)}^{2}}\dfrac{{{y}^{2}}}{{{b}^{2}}}=\dfrac{{{h}^{2}}{{x}^{2}}}{{{a}^{4}}}+\dfrac{{{k}^{2}}{{y}^{2}}}{{{b}^{4}}}+\dfrac{2hkxy}{{{a}^{2}}{{b}^{2}}}\].
Rearranging the terms we get,
\[\Rightarrow \dfrac{{{x}^{2}}}{{{a}^{2}}}\left[ {{\left( \dfrac{{{h}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}} \right)}^{2}}-\dfrac{{{h}^{2}}}{{{a}^{2}}} \right]+\dfrac{{{y}^{2}}}{{{b}^{2}}}\left[ {{\left( \dfrac{{{h}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}} \right)}^{2}}-\dfrac{{{k}^{2}}}{{{b}^{2}}} \right]-\dfrac{2hkxy}{{{a}^{2}}{{b}^{2}}}=0\].
As we can see this equation is of the type $ A{{X}^{2}}+B{{Y}^{2}}+2HXY=0 $ .
We know that, if both lines are perpendicular in $ A{{X}^{2}}+2HXY+B{{Y}^{2}}=0 $ then A+B = 0.
Comparing we get,
 $ \begin{align}
  & A=\left[ {{\left( \dfrac{{{h}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}} \right)}^{2}}-\dfrac{{{h}^{2}}}{{{a}^{2}}} \right]\dfrac{1}{{{a}^{2}}} \\
 & B=\left[ {{\left( \dfrac{{{h}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}} \right)}^{2}}-\dfrac{{{k}^{2}}}{{{b}^{2}}} \right]\dfrac{1}{{{b}^{2}}} \\
\end{align} $ .
Now putting in A+B = 0 we get,
\[\begin{align}
  & \Rightarrow \left[ {{\left( \dfrac{{{h}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}} \right)}^{2}}-\dfrac{{{h}^{2}}}{{{a}^{2}}} \right]\dfrac{1}{{{a}^{2}}}+\left[ {{\left( \dfrac{{{h}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}} \right)}^{2}}-\dfrac{{{k}^{2}}}{{{b}^{2}}} \right]\dfrac{1}{{{b}^{2}}}=0 \\
 & \Rightarrow \left( \dfrac{{{b}^{2}}{{h}^{2}}+{{a}^{2}}{{k}^{2}}}{{{a}^{4}}{{b}^{4}}}-\dfrac{{{h}^{2}}}{{{a}^{2}}} \right)\dfrac{1}{{{a}^{2}}}+\left( \dfrac{{{b}^{2}}{{h}^{2}}+{{a}^{2}}{{k}^{2}}}{{{a}^{4}}{{b}^{4}}}-\dfrac{{{k}^{2}}}{{{b}^{2}}} \right)\dfrac{1}{{{b}^{2}}}=0 \\
 & \Rightarrow \dfrac{{{\left( {{b}^{2}}{{h}^{2}}+{{a}^{2}}{{k}^{2}} \right)}^{2}}}{{{a}^{6}}{{b}^{4}}}-\dfrac{{{h}^{2}}}{{{a}^{4}}}+\dfrac{{{\left( {{b}^{2}}{{h}^{2}}+{{a}^{2}}{{k}^{2}} \right)}^{2}}}{{{a}^{4}}{{b}^{6}}}-\dfrac{{{k}^{2}}}{{{b}^{4}}}=0 \\
 & \Rightarrow \dfrac{{{\left( {{b}^{2}}{{h}^{2}}+{{a}^{2}}{{k}^{2}} \right)}^{2}}}{{{a}^{6}}{{b}^{4}}}+\dfrac{{{\left( {{b}^{2}}{{h}^{2}}+{{a}^{2}}{{k}^{2}} \right)}^{2}}}{{{a}^{4}}{{b}^{6}}}=\dfrac{{{h}^{2}}}{{{a}^{4}}}+\dfrac{{{k}^{2}}}{{{b}^{4}}} \\
\end{align}\].
Taking LCM on right side we get,
\[\Rightarrow \dfrac{{{\left( {{b}^{2}}{{h}^{2}}+{{a}^{2}}{{k}^{2}} \right)}^{2}}}{{{a}^{4}}{{b}^{4}}}\left( \dfrac{1}{{{a}^{2}}}+\dfrac{1}{{{b}^{2}}} \right)=\dfrac{{{h}^{2}}{{b}^{4}}+{{k}^{2}}{{a}^{4}}}{{{a}^{4}}{{b}^{4}}}\]
Taking LCM as \[{{a}^{2}}{{b}^{2}}\] in the bracket term we get,
\[\Rightarrow \dfrac{{{\left( {{b}^{2}}{{h}^{2}}+{{a}^{2}}{{k}^{2}} \right)}^{2}}}{{{a}^{4}}{{b}^{4}}}\left( \dfrac{{{b}^{2}}+{{a}^{2}}}{{{a}^{2}}{{b}^{2}}} \right)=\dfrac{{{h}^{2}}{{b}^{4}}+{{k}^{2}}{{a}^{4}}}{{{a}^{4}}{{b}^{4}}}\]
Cancelling \[{{a}^{4}}{{b}^{4}}\] from denominator on both sides we get,
\[\Rightarrow \dfrac{{{\left( {{b}^{2}}{{h}^{2}}+{{a}^{2}}{{k}^{2}} \right)}^{2}}\left( {{b}^{2}}+{{a}^{2}} \right)}{{{a}^{2}}{{b}^{2}}}={{h}^{2}}{{b}^{4}}+{{k}^{2}}{{a}^{4}}\]
Cross multiplying we get,
\[\Rightarrow {{\left( {{b}^{2}}{{h}^{2}}+{{a}^{2}}{{k}^{2}} \right)}^{2}}\left( {{b}^{2}}+{{a}^{2}} \right)={{a}^{2}}{{b}^{2}}\left( {{h}^{2}}{{b}^{4}}+{{k}^{2}}{{a}^{4}} \right)\]
Rearranging we get,
\[\Rightarrow \left( {{a}^{2}}+{{b}^{2}} \right){{\left( {{b}^{2}}{{h}^{2}}+{{a}^{2}}{{k}^{2}} \right)}^{2}}={{a}^{2}}{{b}^{2}}\left( {{b}^{4}}{{h}^{2}}+{{a}^{4}}{{k}^{2}} \right)\]
Now let us replacing h,k with general variables x,y to get locus, we get,
\[\Rightarrow \left( {{a}^{2}}+{{b}^{2}} \right){{\left( {{b}^{2}}{{h}^{2}}+{{a}^{2}}{{k}^{2}} \right)}^{2}}={{a}^{2}}{{b}^{2}}\left( {{b}^{4}}{{x}^{2}}+{{a}^{4}}{{y}^{2}} \right)\]
Which is our required equation.

Note:
 Students should carefully solve this sum step by step. Take care while comparing the equation by $ A{{X}^{2}}+B{{Y}^{2}}+2HXY=0 $ . Here students often forget $ \dfrac{1}{{{a}^{2}}},\dfrac{1}{{{b}^{2}}} $ terms for A and B. Take care of signs and power of a, b while solving the equation.