Question

Find the locus of midpoint of all chords of the circle $ {{x}^{2}}+{{y}^{2}}-2x=0 $ , such that the pair of lines joining the origin and the extremities of the chord make equal angles with the x – axis.

Answer 1

Hint: To solve this question, we will draw the figure for the given conditions to understand them better. Then we will find the equations of the lines joining the origin and the extremities of the chord. Then, we will solve these line equations with the equation of the given circle to find the point of contacts of the chord. Then we will find the midpoint of these points of contact and eliminate unwanted variables and in the process find the general equation for the midpoint.

Complete step-by-step answer:
The equation of the circle given to us is $ {{x}^{2}}+{{y}^{2}}-2x=0 $
 $ \begin{align}
  & \Rightarrow {{x}^{2}}+{{y}^{2}}-2x+1=1 \\
 & \Rightarrow {{\left( x-1 \right)}^{2}}+{{y}^{2}}=1 \\
\end{align} $
The equation of the circle modifies as $ {{\left( x-1 \right)}^{2}}+{{y}^{2}}=1 $ . Thus, we can say that the centre of the circle lies on (1, 0) and the radius of the circle is 1.
Let C(1, 0) be the centre of the circle and A and B be the point of contact of chord and circle. We will draw lines from origin (0,0) to A and B.

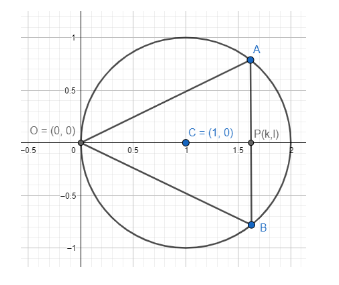
P(k, l) is the midpoint of A and B.
Now, it is given that segment OA and segment OB makes an equal angle with the x – axis.
This means, the slope of the line segments OA and line segment OB is equal. Let that slope be m.
Thus, the equation of the line joining point A and O will be y = mx.
So, to get point A, we need to solve the equation of line segment OA and equation of circle.
Thus, substitute y = mx in equation $ {{x}^{2}}+{{y}^{2}}-2x=0 $
 $ \begin{align}
  & \Rightarrow {{x}^{2}}+{{m}^{2}}x-2x=0 \\
 & \Rightarrow x\left( x+{{m}^{2}}x-2 \right)=0 \\
\end{align} $
x = 0 or $ \begin{align}
  & x\left( 1+{{m}^{2}} \right)-2=0 \\
 & x=\dfrac{2}{1+{{m}^{2}}} \\
\end{align} $
So, x – coordinate of point A will be $ \dfrac{2}{1+{{m}^{2}}} $ .
 $ \Rightarrow $ y = mx
 $ \Rightarrow $ y = $ \dfrac{2m}{1+{{m}^{2}}} $
Thus, coordinates of point A is $ \left( \dfrac{2}{1+{{m}^{2}}},\dfrac{2m}{1+{{m}^{2}}} \right) $ .
Now, the equation of the line joining the point B and O will be y = ─mx.
So, to get point B, we need to solve the equation of line segment OB and equation of circle.
Thus, substitute y = ─mx in equation $ {{x}^{2}}+{{y}^{2}}-2x=0 $
 $ \begin{align}
  & \Rightarrow {{x}^{2}}+{{m}^{2}}x-2x=0 \\
 & \Rightarrow x\left( x+{{m}^{2}}x-2 \right)=0 \\
\end{align} $
So, x – coordinate of point B will be $ \dfrac{2}{1+{{m}^{2}}} $ .
 $ \Rightarrow $ y = ─mx
 $ \Rightarrow $ y = $ -\dfrac{2m}{1+{{m}^{2}}} $
Thus, coordinates of point B is $ \left( \dfrac{2}{1+{{m}^{2}}},-\dfrac{2m}{1+{{m}^{2}}} \right) $ .
Midpoint of A and B is P(k, l).
 $ \Rightarrow $ (k, l) = $ \left( \dfrac{1}{2}\left( \dfrac{2}{1+{{m}^{2}}}+\dfrac{2}{1+{{m}^{2}}} \right),\dfrac{1}{2}\left( \dfrac{2m}{1+{{m}^{2}}}-\dfrac{2m}{1+{{m}^{2}}} \right) \right) $
 $ \Rightarrow $ (k, l) = $ \left( \dfrac{2}{1+{{m}^{2}}},0 \right) $
Thus k = $ \dfrac{2}{1+{{m}^{2}}} $ and l = 0.
Replace k and l with x and y respectively.
Therefore, x = $ \dfrac{2}{1+{{m}^{2}}} $ and y = 0
As the value of m changes, the value of x changes, but y is always equal to zero.
Hence, the required locus is y = 0.

Note: The locus of the midpoint of the required chord is x – axis. If there are two equations of different orders, like a second-degree curve and a line, the best way to solve the equations is through a substitution method.