Question

Find the locus of the circumcenters of the triangle whose two sides are along the coordinate axes and the third side passes through the point of intersection of the lines \[ax + by + c = 0\]and\[lx + my + n = 0\].

Answer 1

Hint: Locus of a point is the set of all points that have the same property or we can say the set of points which behaves in the same way. Circumcenters of the triangle refers to the point in a triangle where all perpendicular bisector of the triangle intersects.
In this question, we have asked to determine the locus of the circumcentre of the triangle such that its two sides are along the coordinate axes and the third side passes through the point of intersection of the lines \[ax + by + c = 0\]and\[lx + my + n = 0\].

Complete step by step answer:
Given that two lines pass through the coordinate axis, hence we can draw the figure as

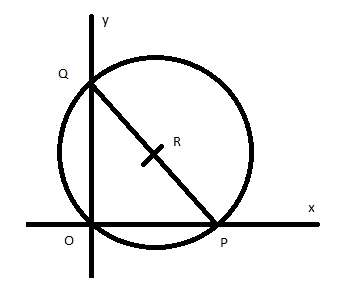
The two lines are perpendicular to each other and the third line passes through the point of intersection of line hence the triangle\[\Delta OPQ\]formed is a right-angle triangle, we know that the circumcenters of a right triangle is the midpoint \[R\left( {h,k} \right)\] of its hypotenuses which is the midpoint of the line PQ, hence
\[
  R\left( {h,k} \right) = \dfrac{{p + 0}}{2},\dfrac{{0 + q}}{2} \\
   = \left( {\dfrac{p}{2},\dfrac{q}{2}} \right) \\
 \]
We can write \[p = 2h\]and\[q = 2k\]
We know the equation of the hypotenuses PQ is\[\dfrac{x}{p} + \dfrac{y}{q} = 1\], hence we can write
 \[
  \dfrac{x}{p} + \dfrac{y}{q} = 1 \\
  \dfrac{x}{{2h}} + \dfrac{y}{{2k}} = 1 \\
  \dfrac{x}{h} + \dfrac{y}{k} = 2 - - - (i) \\
 \]
Given that the hypotenuses passes through the intersecting lines \[ax + by + c = 0\]and\[lx + my + n = 0\]
Now solve both the given equations
\[ax + by + c = 0 - - - - (ii)\]
\[lx + my + n = 0 - - - - (iii)\]
By multiplying (ii) by l and (iii) by a,
\[
  ax + by + c = 0\left. {} \right\} \times l \\
  lx + my + n = 0\left. {} \right\} \times a \\
 \]
We get
\[
  \underline
  alx + bly + cl = 0 \\
  alx\mathop + \limits_ - amy\mathop + \limits_ - an = 0 \\
    \\
  bly - amy + cl - an = 0 \\
    \\
  y\left( {bl - am} \right) = an - cl \\
  y = \dfrac{{an - cl}}{{bl - am}} \\
 \]
Now multiply (ii) by m and (iii) by b
\[
  ax + by + c = 0\left. {} \right\} \times m \\
  lx + my + n = 0\left. {} \right\} \times b \\
 \]
We get
\[
  \underline
   + amx + bmy + cm = 0 \\
  \mathop + \limits_ - blx\mathop + \limits_ - bmy\mathop + \limits_ - bn = 0 \\
    \\
  amx - blx + cm - bn = 0 \\
    \\
  x\left( {am - bl} \right) = bn - cm \\
  x = \dfrac{{an - cl}}{{am - bl}} \\
 \]
Now put the value of x and y in equation (i), we get
\[
  \dfrac{x}{h} + \dfrac{y}{k} = 2 \\
  \dfrac{1}{h}\left( {\dfrac{{an - cl}}{{am - bl}}} \right) + \dfrac{1}{k}\left( {\dfrac{{an - cl}}{{bl - am}}} \right) = 2 \\
    \\
    \\
  \dfrac{{k\left( {an - cl} \right)\left( {bl - am} \right) + h\left( {an - cl} \right)\left( {am - bl} \right)}}{{hk\left( {am - bl} \right)\left( {bl - am} \right)}} = 2 \\
  k\left( {an - cl} \right)\left( {bl - am} \right) + h\left( {an - cl} \right)\left( {am - bl} \right) = 2\left\{ {hk\left( {am - bl} \right)\left( {bl - am} \right)} \right\} \\
  y\left( {an - cl} \right)\left( {bl - am} \right) + x\left( {an - cl} \right)\left( {am - bl} \right) = 2xy\left( {am - bl} \right)\left( {bl - am} \right) \\
    \\
 \]
Hence\[y\left( {an - cl} \right)\left( {bl - am} \right) + x\left( {an - cl} \right)\left( {am - bl} \right) = 2xy\left( {am - bl} \right)\left( {bl - am} \right)\] is the equation for the locus of the circumcenter of the circle.

Note: Locus can be a set of points, lines, line segments, curve, and surface which satisfy one or more properties. In the case of a right-angled triangle, the circumcenter of the triangle is always the midpoint of hypotenuses of that triangle.