Question

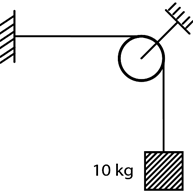
Find the magnitude of force exerted on string by pulley.

Answer 1

Hint: The normal reaction would be balancing the forces of tension from string on left and downward sides. So, it would equal the opposite of the resultant tension forces.

Complete step by step answer:First we will draw the F.B.D of the box and the pulley. As we can see from the question diagram, there would be two forces acting on the box- tension due to string (say T) in the upward direction and weight (say mg) in the downward direction. On the pulley there would be three forces, tension due to string towards left and down , and normal reaction towards string. The tension would be the same as the tension on the box from string because the string is uniform and doesn’t undergo any knot or blockage. Let the tensions be T and normal reactions be N.

 

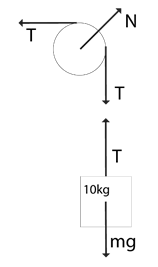
Now, considering equilibrium we can apply the equilibrium condition.
On box,
 $\sum {{F_x} = 0} $
There are no forces in x-direction.
For y direction,
 $
  \sum {{F_y} = 0} \\
   \Rightarrow T = mg \\
   \Rightarrow T = 10kg \times 10m/s \\
   \Rightarrow T = 100N \\
 $
On pulley, normal reaction can be divided in rectangular components in x-y plane as
 

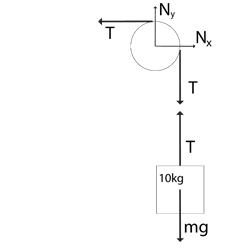
Now balancing the forces in x and y directions, we get
$
  \sum {{F_x} = 0} \\
   \Rightarrow {N_x} = T \\
 $
 $
  \sum {{F_y}} = 0 \\
   \Rightarrow {N_y} = T \\
 $
Therefore, normal reaction would be the vector sum of normal reaction components in x and y direction.
$
  N = \sqrt {N_x^2 + N_y^2} \\
   \Rightarrow N = \sqrt {{T^2} + {T^2}} = T\sqrt 2 \\
   \Rightarrow N = 100\sqrt 2 {\rm N} \\
 $
Therefore, the correct answer is the pulley exerts a force of $100\sqrt 2 {\rm N}$ on the string.

Note:We can also first calculate the total tension forces on the pulley and then equate it to the normal reaction force i.e. ${T_{total}} = \sqrt {{T^2} + {T^2}} = T\sqrt 2 = N$ .