Question

Find the measure of each interior angle of a regular polygon of 9 sides.
A. \[160^\circ\]
B. \[180^\circ\]
C. \[120^\circ\]
D. \[140^\circ\]

Answer 1

Hint: In this problem, we need to use the formula for the interior angle of a regular polygon of \[n\] sides. Next, substitute 9 for \[n\] in the formula of interior angle and solve.

Complete step by step answer:
All the interior angles of a regular polygon are equal. The minimum interior angle of a regular polygon is 60 degree. An exterior angle of a polygon is an angle outside the polygon formed by one of its sides and the extension of an adjacent side.
The formula for the interior angle of a regular polygon of \[n\] sides is shown below.
\[{\text{interior angle = }}\dfrac{{180\left( {n - 2} \right)}}{n}\]

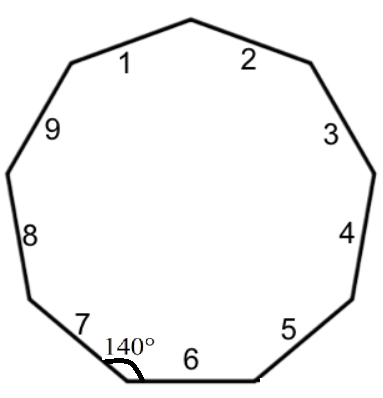
Now, substitute 9 for \[n\] in the above formula to obtain the interior angle of a regular polygon of side 9.
\[
  \,\,\,\,\,\,{\text{interior angle = }}\dfrac{{180\left( {9 - 2} \right)}}{9} \\
   \Rightarrow {\text{interior angle = }}\dfrac{{180\left( 7 \right)}}{9} \\
   \Rightarrow {\text{interior angle = }}20\left( 7 \right) \\
   \Rightarrow {\text{interior angle = }}140^\circ \\
\]

So, the correct answer is “Option D”.

Note: A polygon is a two-dimensional shape formed with identical straight lines oriented at different positions. A regular polygon is a closed geometry whose all sides and angles are equal. It is required to have at least three sides to form a regular polygon. The formula for the interior angle of a regular polygon having \[n\] sides is \[\dfrac{{180\left( {n - 2} \right)}}{n}\].