Question

Find the measure of each interior angle of a regular polygon of 5 sides.

Answer 1

Hint: Use the formula for calculating the measure of each interior angle of a regular polygon, which is given by \[\left( n-2 \right)\dfrac{{{180}^{\circ }}}{n}\], where n represents the number of sides of the regular polygon. One must remember that in a regular polygon, all the sides are of equal length. Use the fact that angles opposite to equal sides are also equal to prove that all the angles of a regular polygon are equal as well.

Complete Step-by-step answer:
We have to calculate the measure of each interior angle of a regular polygon of 5 sides.
We know that angles opposite to equal sides are also equal.
As all the sides of a regular polygon are equal, all the angles have equal measure as well.

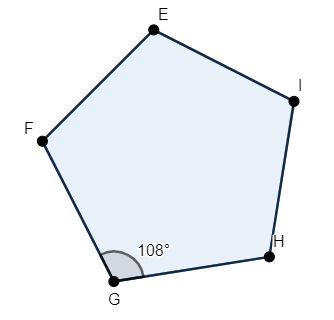
We know that a regular polygon with ‘n’ sides has the measure of each angle equal to \[\left( n-2 \right)\dfrac{{{180}^{\circ }}}{n}\].
Substituting \[n=5\] in the above formula, the measure of each angle \[=\left( 5-2 \right)\dfrac{{{180}^{\circ }}}{5}=\dfrac{3}{5}\left( {{180}^{\circ }} \right)={{108}^{\circ }}\].
Hence, the value of each angle of a regular polygon with 5 sides is \[{{108}^{\circ }}\].

Note: A regular polygon is defined as a flat shape whose sides are all equal in length and whose angles are all equal. A regular polygon having 5 sides is called a pentagon. The sum of internal angles of a regular polygon is \[\left( n-2 \right){{180}^{\circ }}\]. Thus, for a pentagon, the sum of measures is \[{{540}^{\circ }}\]. The sum of all exterior angles of a regular polygon is \[{{180}^{\circ }}\]. The diagonals of a convex regular polygon are in the golden ratio to its sides. One must be careful while calculating the value of interior angles. We will get different measures of angles when measured in degrees and radians.