Question

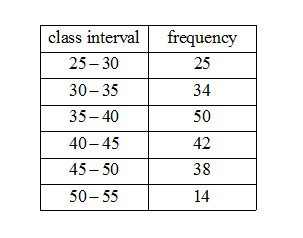
Find the mode of following frequency distribution. \[\]

Answer 1

Hint: We use the fact that if the data is in groups or class interval , the modal interval ${{I}_{m}}$corresponds to highest frequency ${{f}_{m}}$. We then use the formula for the mode $M$$M=L+\dfrac{{{f}_{m}}-{{f}_{m-1}}}{\left( {{f}_{m}}-{{f}_{m-1}} \right)\left( {{f}_{m}}-{{f}_{m+1}} \right)}\times w$ where L is the lower boundary, $w$ is the width of the modal interval ${{I}_{m}}$, ${{f}_{m-1}},{{f}_{m+1}}$ are the frequencies of the class intervals ${{I}_{m-1}},{{I}_{m+1}}$ respectively. \[\]

Complete step by step answer:
We know that mode is a measure of the central tendency of the data or population. It expresses just like mean and median the most important value towards which all the data points show a tendency. The highest value in the data is called mode. If there are $n$ data points say ${{x}_{1}},{{x}_{2}},...,{{x}_{n}}$ then $M$ is will be the mode and if only if
\[M>{{x}_{i}},i=1,2,3...n\]
It may also happen that the highest value of $M$ may occur several times. So in accordance, we call the data unimodal if $M$ occurs only once, bimodal if $M$ occurs twice, trimodal if $M$ occurs thrice, and so on.
When we have the data in groups or class intervals we first find the modal interval which corresponds to highest frequency . If the grouped data has $n$ intervals say ${{I}_{1}},{{I}_{2}},...,{{I}_{n}}$ and their corresponding frequencies${{f}_{1}},{{f}_{2}},..{{f}_{n}}$, then ${{I}_{m}},m=1,2,..n$ will be the modal interval if ${{I}_{m}}$ has the frequency ${{f}_{m}}$ such that
\[{{f}_{m}}>{{f}_{i}},i=1,2,..n\]
We then estimate the mode using the following formula and conclude whether ${{I}_{m}}$ is the modal interval or not.
\[M=L+\dfrac{{{f}_{m}}-{{f}_{m-1}}}{\left( {{f}_{m}}-{{f}_{m-1}} \right)\left( {{f}_{m}}-{{f}_{m+1}} \right)}\times w\]

Here L is the lower boundary, $w$ is the width of the modal interval. The frequency${{f}_{m-1}}$ is the frequency corresponding to the interval right before ${{I}_{m}}$ that is ${{I}_{m-1}}$ and the frequency ${{f}_{m+1}}$ is the frequency corresponding to the interval right after ${{I}_{m}}$ that is ${{I}_{m+1}}$.
So let us observe the data given in the question. \[\]

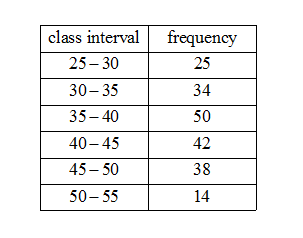
We see the highest frequency is 50 and its corresponding interval is 35-50. So we have ${{f}_{m}}=50$the modal interval ${{I}_{m}}=\left[ 35,40 \right]$. The width of ${{I}_{m}}$is $w=40-35=5$ and the lower boundary of ${{I}_{m}}$is $L=35$. The frequency of ${{I}_{m-1}}$ is ${{f}_{m-1}}=34$ and of ${{I}_{m+1}}$ is ${{f}_{m-1}}=42$.Now we estimate the mode using the formula. We have,
\[\begin{align}
  & M=35+\dfrac{50-34}{\left( 50-34 \right)\left( 50-42 \right)}\times 5 \\
 & =35+\dfrac{6}{6\times 8}\times 5 \\
 & =35+.625=35.625 \\
\end{align}\]
We see that the estimated mode lie in the interval ${{I}_{m}}=\left[ 35,40 \right]$. So the mode is $\left[ 35,40 \right]$\[\]
Note:
 If the frequency 50 would have occurred more than once we would more than modal intervals. The mean of the class interval data is determined using the formula $\mu =\dfrac{\sum\limits_{i=1}^{n}{{{f}_{i}}{{x}_{i}}}}{\sum\limits_{i=1}^{n}{{{f}_{i}}}}$ where${{x}_{i}}$ is the midpoint of the interval ${{I}_{i.}}$ The median is the interval that corresponds to $\dfrac{\sum\limits_{i=1}^{n}{{{f}_{i}}}}{2}$.