Question

Find the moment of inertia of a uniform square plate of mass m and edge an about one of its diagonals.

Answer 1

Hint: The moment of inertia of a point mass with respect to an axis is defined as the product of the mass times the distance from the axis squared. So, for defining the moment of inertia first of all we have to define the point around which the body would rotate when torque acts on it.

Complete step by step answer:We need to find the moment of inertia of a uniform square plate of given mass m, so we assume our square to be placed on the x-axis and let the side of the square be a.

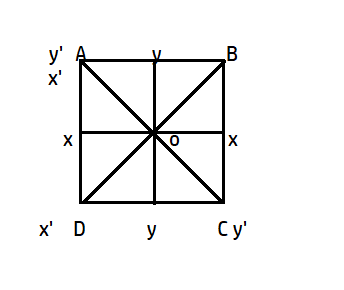
Mass of square=m
Side of square= a
Mass per unit area= \[\dfrac{m}{{{a}^{2}}}\]
Let the small cross-section area be at some distance x from the x-axis, let the width of this small area be dx and length be a.
So, the area of this small cross-section is \[adx\]
Mass of this small cross-section is \[\dfrac{m}{{{a}^{2}}}\times adx=\dfrac{mdx}{a}\]
So the moment of inertia about xx axis is given by,
\[{{I}_{xx}}=2\int\limits_{0}^{0.5a}{\dfrac{mdx}{a}\times {{x}^{2}}}=\dfrac{2m}{a}[\dfrac{{{x}^{3}}}{3}]_{0}^{0.5a}=\dfrac{m{{a}^{2}}}{12}\]
Here we have multiplied the integral by 2 because we have divided the square into 4 smaller areas and 2 of them lie at x-axis.
Now using a theorem of the parallel axis,
\[\begin{align}
  & {{I}_{zz}}={{I}_{x'x'}}+{{I}_{yy}} \\
 & =2\times \dfrac{m{{a}^{2}}}{12} \\
 & =\dfrac{m{{a}^{2}}}{6} \\
\end{align}\]
Since the two diagonals are perpendicular to each other, therefore \[{{I}_{zz}}={{I}_{x'x'}}+{{I}_{y'y'}}\]
\[\dfrac{m{{a}^{2}}}{6}=2\times {{I}_{x'x'}}\]
This is because \[{{I}_{x'x'}}={{I}_{y'y'}}\]
So, the moment of inertia of a uniform square plate of mass m and edge an about one of its diagonals comes out to be \[\dfrac{m{{a}^{2}}}{12}\]

Note:
Moment of inertia is the name given to rotational inertia, and it plays the same role in rotation as is played by mass in translation. Moment of inertia is defined concerning a specific rotation axis. Here we have defined concerning the diagonal. We could have also defined it about the geometrical centre.