Question

Find the moment of inertia of the triangular lamina of mass M and about the axis of rotation AA’ shown in the figure:

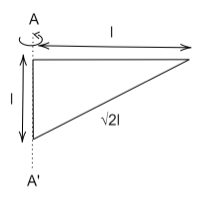
Answer 1

Hint: To find the moment of inertia, a small element is assumed to be situated in the body of the lamina and is integrated, by putting the end points of the triangle as upper and lower limits. And then the moment of inertia is calculated by keeping the appropriate values obtained.

Formula used:
$I = M{r^2}$
Where M is the total mass of the object and r is the distance from the axis of rotation.

Complete step by step answer:
To find the moment of inertia of the lamina, we first assume a very small rectangular area of width dx at a distance x from the axis of the triangle.

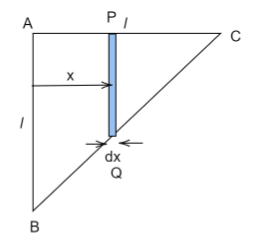
Let the mass per unit area of the lamina be $\sigma $then it is defined as:
$\sigma = \dfrac{M}{A}$
The area of a triangle is given by
$A = \dfrac{1}{2}b \times h$
Where b and h are base and height of the triangle.
For this triangle, base is equal to height and both are $ = l$
Therefore,$A = \dfrac{1}{2}{l^2}$
We can write-
$\sigma = \dfrac{{2M}}{{{l^2}}}$
From the diagram, the triangles $\vartriangle ABC \sim \vartriangle PQC$
(Similar triangles)
So it can be said that,
$\dfrac{{AC}}{{PC}} = \dfrac{{AB}}{{PQ}}$
It is given that
$AC = l$
$ \Rightarrow PC = l - x$
$ \Rightarrow AB = l$
Therefore PQ can be written as-
$\dfrac{l}{{l - x}} = \dfrac{l}{{PQ}}$
$ \Rightarrow PQ = l - x$
The area of the small rectangular element can be given by
$dA = L \times B$
Where L is the length and B is the breadth.
$dA = (l - x)dx$
The moment of inertia for this rectangular element can be given by,
$dI = \int {{x^2}dm} $
Where dm is the mass of the small element, this mass can be rewritten in terms of mass density and area,
So we have,
$dm = \sigma dA$
$ \Rightarrow \int {dI} = \int {\sigma (1 - x).{x^2}dx} $
We also have,
$\sigma = \dfrac{{2M}}{{{l^2}}}$
$ \Rightarrow \int {dI = \dfrac{{2M}}{{{l^2}}}\int\limits_0^l {(l - x).{x^2}dx} } $
It can be expanded into-
$\smallint dI = \dfrac{{2M}}{{{l^2}}}\int\limits_0^l {l{x^2}} - \int\limits_0^l {{x^3}} dx$
After integrating,
\[I = \dfrac{{2M}}{{{l^2}}}\left( {\left[ {\dfrac{{l{x^3}}}{3}} \right]_0^l - \left[ {\dfrac{{{x^4}}}{4}} \right]_0^l} \right)\]
\[ \Rightarrow I = \dfrac{{2M}}{{{l^2}}}\left[ {\left( {\dfrac{{{l^4}}}{3}} \right) - \left( {\dfrac{{{l^4}}}{4}} \right)} \right]\]
Taking l common from the terms containing it,
\[I = \dfrac{{2M{l^4}}}{{{l^2}}}\left[ {\left( {\dfrac{1}{3}} \right) - \left( {\dfrac{1}{4}} \right)} \right]\]
$ \Rightarrow I = 2M{l^2}\left( {\dfrac{{4 - 3}}{{12}}} \right)$
$ \therefore I = \dfrac{{M{l^2}}}{6}$

The inertia of the given lamina about AA’ axis is $I = \dfrac{{M{l^2}}}{6}$.

Note:Moment of inertia tells us about how easy it is to rotate an object about the given axis. Apart from the mass of the object, it depends on the distance from the axis around which it is rotated. If the mass of the object is a function of its length, area or volume, the formula of moment of inertia is adjusted accordingly before integrating.However in the question,only the distribution of mass is calculated as the total mass of the triangular lamina is already given to us.