Question

Find the number of points on the straight line with points (-4, 11) to (16,-1) whose coordinates are positive integers?

Answer 1

Use the equation of a straight line which passes through two given points that is $y - {y_1} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\left( {x - {x_1}} \right)$,where $({x_1},{y_1}){\text{ and (}}{{\text{x}}_2},{y_2})$are the passing points. The points whose coordinates are positive can be taken out by considering all the points on the straight line which are in the first quadrant.

Complete step by step answer:

Given points (-4, 11) and (16, -1)
So first find out the equation of line passing through these two points.

As we know the equation of line passing through the two points is given as
$y - {y_1} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\left( {x - {x_1}} \right)$
Let A = (x1, y1) = (-4, 11)
B = (x2, y2) = (16, -1)

So the equation of line is
$ \Rightarrow y - 11 = \dfrac{{ - 1 - 11}}{{16 + 4}}\left( {x - \left( { - 4} \right)} \right)$

Now simplify the above equation we have,
$ \Rightarrow y - 11 = \dfrac{{ - 12}}{{20}}\left( {x + 4} \right)$
$ \Rightarrow y - 11 = \dfrac{{ - 3}}{5}\left( {x + 4} \right)$………………… (1)
$ \Rightarrow 5y - 55 = - 3x - 12$
$ \Rightarrow 3x + 5y = 43$…………………. (2)

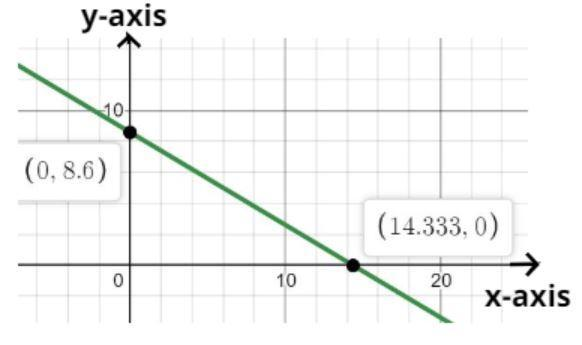
Now plot this equation on the coordinate axis which is shown above
Now we have to find out the points whose coordinates are positive integers (i.e. x and y both are positive).

And we all know x and y both are positive in the first quadrant so the points lie in the first quadrant.
Now when we put x = 0 in the equation we get y = (43/5) (see figure) so the point is (0, 8.6) and when we put y = 0 in the equation we get x = (43/3) see figure so the point is (14.333, 0) but we have to find out all the integer points which satisfy the equation in first quadrant.

So x belongs from (0 < x < 14.333) …………………… (3)
And y belongs from (0 < y < 8.6)………………………. (4)

Now from equation (1)
$ \Rightarrow y - 11 = \dfrac{{ - 3}}{5}\left( {x + 4} \right)$ y is an integer when (x + 4) is a multiple of 5.

So the possible of x is (1 + 4 =5), (6 + 4 = 10), (11 + 4) =15 we cannot take further values of x according to equation (3)

So possible x = 1, 6 and 11

So for these values calculate the values of y
For x = 1,
y = (11 – 3) = 8
For x = 6,
$y = 11 - \dfrac{3}{5}\left( {10} \right) = 11 - 6 = 5$

For x= 11,
$y = 11 - \dfrac{3}{5}\left( {15} \right) = 11 - 9 = 2$
So all their values of y satisfies the equation (4).

So the number of points on the straight line whose coordinates are positive integer are,
(1, 8), (6, 5) and (11, 2)

So there are 3 points on the straight line whose coordinates are positive integers.

So this is the required answer.

Note – The diagrammatic representation using the equation of the line always helps in understanding the basic figure and the quadrants through which a line passes. The coordinate where a line cuts x axis is where the y coordinate of line is zero as on x axis y is zero, similarly the coordinate where a line cuts x axis is where the y coordinate of line is zero as on x axis y is zero.