Question

Find the number of sides in a regular polygon if each interior angle is eight times the adjacent exterior angle.

Answer 1

Hint: To solve the given question, we will first find out the relation between the interior angle and the exterior angle. Now, we will make use of the fact that the sum of the interior and adjacent exterior angle is \[{{180}^{o}}.\] From here, we will find the value of the interior angle. Now, we will divide the polygon into the triangles and here we will find the angle subtended by each side on the center with the help of the fact that the sum of the angles in a triangle is \[{{180}^{o}}.\] Then to obtain the total number of sides, we will divide \[{{360}^{o}}\] by this angle obtained.

Complete step by step answer:
For a better understanding of the question, we will draw a rough sketch of n – sided polygon.

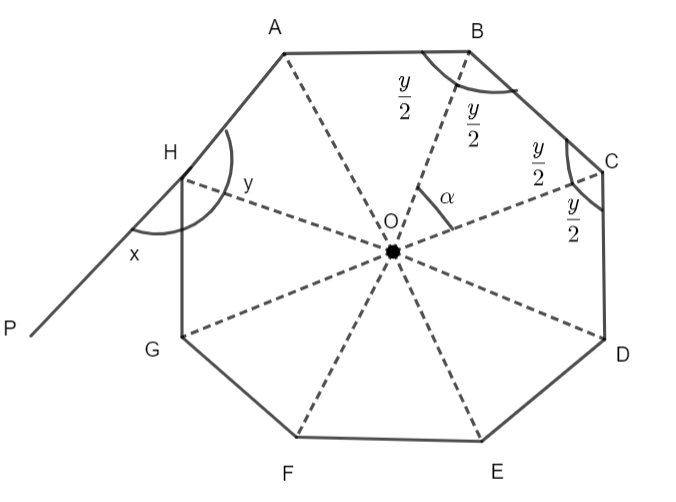
Here, we have drawn the n – sided polygon and x is the exterior angle and y is the adjacent interior angle. Now, we know that the sum of the interior angle and the exterior angle is \[{{180}^{o}}\] (because AP is a straight line), so we will get,
\[x+y={{180}^{o}}....\left( i \right)\]
Now, it is given in the question that the interior angle is 8 times the exterior angle. Thus, we can say that,
\[y=8x....\left( ii \right)\]
From (i) and (ii), we can say that,
\[\Rightarrow x+8x={{180}^{o}}\]
\[\Rightarrow 9x={{180}^{o}}\]
\[\Rightarrow x={{20}^{o}}...\left( iii \right)\]
Now, we will put the value of \[x={{20}^{o}}\] in equation (ii). Thus, we will get,
\[\Rightarrow y=8\left( {{20}^{o}} \right)\]
\[\Rightarrow y={{160}^{o}}....\left( iv \right)\]
Now, O is the center of the polygon and the polygon is divided into n triangles such that each side subtends an angle of \[\alpha \] on the center. Now, we will consider the triangle BOC. We know that, in a triangle, the sum of the interior angles is \[{{180}^{o}}.\] Thus, we will get,
\[\Rightarrow a+\dfrac{y}{2}+\dfrac{y}{2}={{180}^{o}}\]
\[\Rightarrow a+y={{180}^{o}}\]
\[\Rightarrow a+{{160}^{o}}={{180}^{o}}\left[ \text{From iv} \right]\]
\[\Rightarrow a={{20}^{o}}....\left( v \right)\]
Now, there are n sided and each side subtends an angle \[\alpha \] in the center. Also, we know that the total angle subtended on the center is \[{{360}^{o}}.\] Thus, we will get,
\[n\alpha ={{360}^{o}}\]
\[\Rightarrow n\left( {{20}^{o}} \right)={{360}^{o}}\left[ \text{From v} \right]\]
\[\Rightarrow n=\dfrac{{{360}^{o}}}{{{20}^{o}}}\]
\[\Rightarrow n={{18}^{o}}\]
So, there are 18 sides in the given polygon.

Note: We can also solve the above question in an alternate way which is as shown below: If the number of sides of a polygon is given, then the interior angle of that polygon is given by the formula,
\[\text{Interior Angle}=\left( \dfrac{n-2}{n} \right)\times {{180}^{o}}\]
In our case, the interior angle is calculated by us and it is \[y={{160}^{o}}.\] Thus, we have,
\[{{160}^{o}}=\left( \dfrac{n-2}{n} \right)\times {{180}^{o}}\]
\[\Rightarrow \dfrac{n-2}{n}=\dfrac{{{160}^{o}}}{{{180}^{o}}}\]
\[\Rightarrow 9n-18=8n\]
\[\Rightarrow n=18\]