Question

Find the number of solutions of the equation tanx +secx = 2cosx in the interval $\left[ 0,2\pi \right]$

Answer 1

Hint: Convert tanx and secx into sines and cosines using $\tan x=\dfrac{\sin x}{\cos x}$ and $\sec x=\dfrac{1}{\cos x}$. Use ${{\cos }^{2}}x=1-{{\sin }^{2}}x$ and ${{a}^{2}}-{{b}^{2}}=\left( a+b \right)\left( a-b \right)$ to factorise the expression. Using zero product property form two trigonometric equations. Find the solutions of those equations in $\left[ 0,2\pi \right]$ and hence find the total number of solutions of the original equation in $\left[ 0,2\pi \right]$.

Complete Step-by-step answer:
We have LHS $=\tan x+\sec x$
We know that $\tan x=\dfrac{\sin x}{\cos x}$ and $\sec x=\dfrac{1}{\cos x}$.
Using the above formulae, we get
LHS = $\dfrac{\sin x}{\cos x}+\dfrac{1}{\cos x}$
Hence the equation becomes
$\dfrac{\sin x}{\cos x}+\dfrac{1}{\cos x}=2\cos x$
Taking cosx LCM on LHS, we get
$\dfrac{\sin x+1}{\cos x}=2\cos x$
Multiplying both sides by cosx, we get
$\sin x+1=2{{\cos }^{2}}x$
We know that ${{\cos }^{2}}x=1-{{\sin }^{2}}x$
Hence we have
$\sin x+1=2\left( 1-{{\sin }^{2}}x \right)$
We know that ${{a}^{2}}-{{b}^{2}}=\left( a-b \right)\left( a+b \right)$
Hence, we have
$1-{{\sin }^{2}}x=\left( 1+\sin x \right)\left( 1-\sin x \right)$
Hence we have
$1+\sin x=2\left( 1-\sin x \right)\left( 1+\sin x \right)$
Transposing terms on RHS to LHS, we get
$1+\sin x-2\left( 1-\sin x \right)\left( 1+\sin x \right)=0$
Taking 1+sinx common, we get
$\begin{align}
  & \left( 1+\sin x \right)\left( 1-2\left( 1-\sin x \right) \right)=0 \\
 & \Rightarrow \left( 1+\sin x \right)\left( 2\sin x-1 \right)=0 \\
\end{align}$
We know that if ab = 0, then a = 0 or b = 0 (Zero product property)
Hence we have
$1+\sin x=0$ or $2\sin x-1=0$
Solving 1+sinx = 0:
Subtracting 1 from both sides, we get
sinx =-1
We know that $\sin \left( \dfrac{3\pi }{2} \right)=-1$
Hence, we have
$\sin x=\sin \left( \dfrac{3\pi }{2} \right)$
We know that the general solution of the equation $\sin x=\sin y$ is given by $x=n\pi +{{\left( -1 \right)}^{n}}y$
Hence we have $x=n\pi +{{\left( -1 \right)}^{n}}\dfrac{3\pi }{2}$
Hence if $x\in \left[ 0,2\pi \right]$, we have $x=\dfrac{3\pi }{2}$
Solving 2sinx-1=0:
Adding 1 on both sides, we get
$2\sin x=1$
Dividing by 2 on both sides, we get
$\sin x=\dfrac{1}{2}$
We know that $\sin \left( \dfrac{\pi }{6} \right)=\dfrac{1}{2}$
Hence we have
$\sin x=\sin \left( \dfrac{\pi }{6} \right)$
Now we know that the general solution of the equation $\sin x=\sin y$ is given by $x=n\pi +{{\left( -1 \right)}^{n}}y,n\in \mathbb{Z}$
Hence we have
$x=n\pi +{{\left( -1 \right)}^{n}}\dfrac{\pi }{6}$
Taking n = 0, 1 we get
$x=\dfrac{\pi }{6},\dfrac{5\pi }{6}$
Note that when $x=\dfrac{3\pi }{2}$ cosx = 0 and hence tanx and secx do not exist.
Hence the only solutions are $x=\dfrac{\pi }{6},\dfrac{5\pi }{6}$.
Hence the number of solutions of the equation $\tan x+\sec x=2\cos x$ in the interval $\left[ 0,2\pi \right]$ is two.

Note: [1] Do not forget to check whether each of the roots is in the domain or not. Failure to do so often leads to incorrect results in solving trigonometric equations.
Hence it is very important to check each of the roots in the original equation.
[2] The graph of tanx +secx (green) and 2cosx (blue) are plotted below:

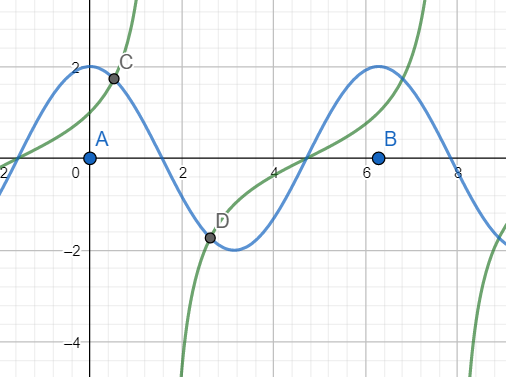
As is evident from the graph in the interval$\left[ A=0,B=2\pi \right]$, only two solutions exist: C and D.