
Find the order of rotational symmetry of rhombus.
A.4
B. 3
C.2
D.1
Answer
487.2k+ views
1 likes
Hint: We recall the definition of center of rotation, rotational symmetry of planar objects which are rotated by angles, the order of rotational symmetry as the number of times the object will look exactly like the object in the initial position. We rotate the rhombus by
Complete step-by-step solution
We know that rotation is geometric operation mathematics where an object in motion preserves at least one point. If the rotation is only around only one preserved point which happens only for planar objects we call that point center of rotation.
We know that we call an object rationally symmetrical when the object is invariant of rotation which means if we rotate the object by a partial turn, the object looks the same.
The planar objects are rotated by an angle, and we know that for regular polygons the center of rotation is the point of intersection of diagonals. The order of rotational symmetry is the number of times the object looks when it is rotated by a full turn which is in-plane by an angle of
The rhombus is a regular polygon with four equal sides. Let ABCD be rhombus with O as the point of intersection of diagonals.
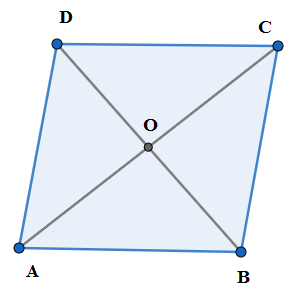
We know that the diagonals of a rhombus are perpendicular to each other whose point of intersection is the center of rotation. So we rotate the rhombus ABCD about O by right angle
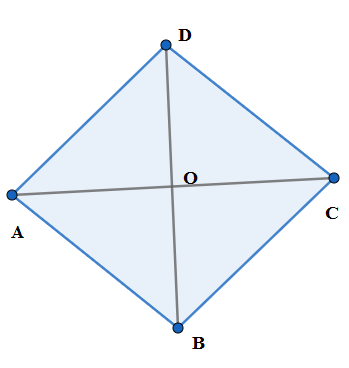
We see that the above figure does not look like the initial figure of the rhombus. So we rotate again by
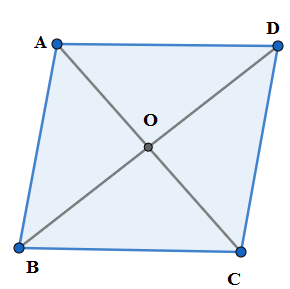
We see that the above figure looks like the initial figure of the rhombus. We rotate again by
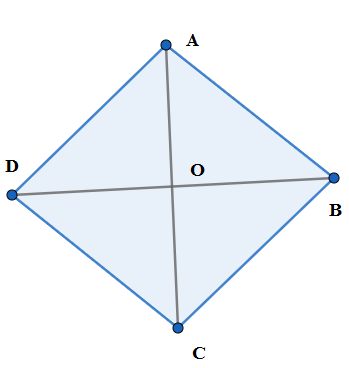
We see that the above figure does not look like the initial figure of the rhombus. So we rotate again by
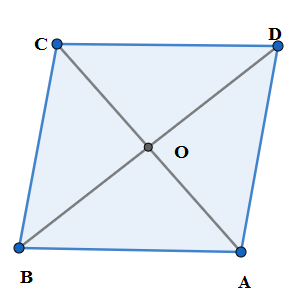
We see that the above figure looks like the initial figure of the rhombus. We have rotated a complete turn of angle
So the order of rotational symmetry for the rhombus is 2 and the correct option is C.
Note: We note that the initial position of the rhombus is at a rotational angle of
Complete step-by-step solution
We know that rotation is geometric operation mathematics where an object in motion preserves at least one point. If the rotation is only around only one preserved point which happens only for planar objects we call that point center of rotation.
We know that we call an object rationally symmetrical when the object is invariant of rotation which means if we rotate the object by a partial turn, the object looks the same.
The planar objects are rotated by an angle, and we know that for regular polygons the center of rotation is the point of intersection of diagonals. The order of rotational symmetry is the number of times the object looks when it is rotated by a full turn which is in-plane by an angle of
The rhombus is a regular polygon with four equal sides. Let ABCD be rhombus with O as the point of intersection of diagonals.

We know that the diagonals of a rhombus are perpendicular to each other whose point of intersection is the center of rotation. So we rotate the rhombus ABCD about O by right angle

We see that the above figure does not look like the initial figure of the rhombus. So we rotate again by

We see that the above figure looks like the initial figure of the rhombus. We rotate again by

We see that the above figure does not look like the initial figure of the rhombus. So we rotate again by

We see that the above figure looks like the initial figure of the rhombus. We have rotated a complete turn of angle
So the order of rotational symmetry for the rhombus is 2 and the correct option is C.
Note: We note that the initial position of the rhombus is at a rotational angle of
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Trending doubts
Full Form of IASDMIPSIFSIRSPOLICE class 7 social science CBSE

Whom did king Ashoka send to Sri Lanka to spread Buddhism class 7 social science CBSE

The southernmost point of the Indian mainland is known class 7 social studies CBSE

How many crores make 10 million class 7 maths CBSE

AIM To prepare stained temporary mount of onion peel class 7 biology CBSE

Find HCF and LCM of 120 and 144 by using Fundamental class 7 maths CBSE





